


Next: The ACCL algorithm
Up: Learning with Mixtures of
Previous: The SPLICE dataset: Feature
The accelerated tree learning algorithm
We have argued that the mixture of trees approach has significant
advantages over general Bayesian networks in terms of its algorithmic
complexity. In particular, the M step of the EM algorithm for
mixtures of trees is the CHOWLIU algorithm, which scales
quadratically in the number of variables 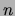 and linearly in the
size of the dataset
and linearly in the
size of the dataset 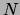 . Given that the E step is linear in
. Given that the E step is linear in 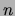 and
and 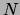 for mixtures of trees, we have a situation in which each
pass of the EM algorithm is quadratic in
for mixtures of trees, we have a situation in which each
pass of the EM algorithm is quadratic in 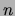 and linear in
and linear in 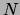 .
Although this time complexity recommends the MT approach for
large-scale problems, the quadratic scaling in
.
Although this time complexity recommends the MT approach for
large-scale problems, the quadratic scaling in 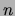 becomes problematic
for particularly large problems. In this section we propose a method
for reducing the time complexity of the MT learning algorithm and
demonstrate empirically the large performance gains that we are able
to obtain with this method.
As a concrete example of the kind of problems that we have in mind,
consider the problem of clustering or classification of documents in
information retrieval. Here the variables are words from a vocabulary,
and the data points are documents. A document is represented as a binary
vector with a component equal to 1 for each word
becomes problematic
for particularly large problems. In this section we propose a method
for reducing the time complexity of the MT learning algorithm and
demonstrate empirically the large performance gains that we are able
to obtain with this method.
As a concrete example of the kind of problems that we have in mind,
consider the problem of clustering or classification of documents in
information retrieval. Here the variables are words from a vocabulary,
and the data points are documents. A document is represented as a binary
vector with a component equal to 1 for each word  that is present
in the document and equal to 0 for each word
that is present
in the document and equal to 0 for each word  that is not present.
In a typical application the number of documents
that is not present.
In a typical application the number of documents 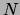 is of the
order of
is of the
order of 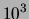 -
- 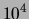 , as is the vocabulary size
, as is the vocabulary size 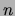 .
Given such numbers, fitting a single tree to the data requires
.
Given such numbers, fitting a single tree to the data requires
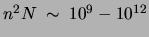 counting operations.
Note, however, that this domain is characterized by a certain
sparseness: in particular, each document contains only a
relatively small number of words and thus most of the components
of its binary vector are 0.
In this section, we show how to take advantage of data sparseness to
accelerate the CHOWLIU algorithm. We show that in the sparse
regime we can often rank order mutual information values without
actually computing these values. We also show how to speed up
the computation of the sufficient statistics by exploiting
sparseness. Combining these two ideas yields an algorithm--the
ACCL (accelerated Chow and Liu) algorithm--that provides
significant performance gains in both running time and memory.
counting operations.
Note, however, that this domain is characterized by a certain
sparseness: in particular, each document contains only a
relatively small number of words and thus most of the components
of its binary vector are 0.
In this section, we show how to take advantage of data sparseness to
accelerate the CHOWLIU algorithm. We show that in the sparse
regime we can often rank order mutual information values without
actually computing these values. We also show how to speed up
the computation of the sufficient statistics by exploiting
sparseness. Combining these two ideas yields an algorithm--the
ACCL (accelerated Chow and Liu) algorithm--that provides
significant performance gains in both running time and memory.
Subsections



Next: The ACCL algorithm
Up: Learning with Mixtures of
Previous: The SPLICE dataset: Feature
Journal of Machine Learning Research
2000-10-19