


Next: Memory requirements
Up: The ACCL algorithm
Previous: The algorithm and its
The algorithm requires: 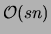 for computing
for computing
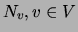 ,
,
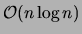 for sorting the variables,
for sorting the variables,
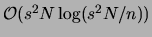 for step 2,
for step 2, 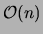 for step 3,
for step 3,
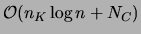 for the Kruskal algorithm (
for the Kruskal algorithm (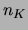 is the
number of edges examined by the algorithm,
is the
number of edges examined by the algorithm, 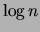 is the time for an
extraction from
is the time for an
extraction from 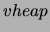 ,
, 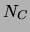 is an upper bound for the number of
elements in the lists
is an upper bound for the number of
elements in the lists
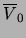 whose elements need to be
skipped occasionally when we extract variables from the virtual lists
whose elements need to be
skipped occasionally when we extract variables from the virtual lists
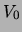 ), and
), and 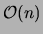 for creating the the
for creating the the 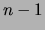 probability tables in
step 5. Summing these terms, we obtain the following upper bound for
the running time of the acCL algorithm:
probability tables in
step 5. Summing these terms, we obtain the following upper bound for
the running time of the acCL algorithm:
If we ignore the logarithmic factors this simplifies to
For constant 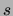 , this bound is a polynomial of degree 1 in the
three variables
, this bound is a polynomial of degree 1 in the
three variables 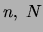 and
and 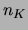 . Because
. Because 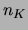 has the range
has the range
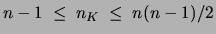 , the worst case
complexity of the ACCL algorithm is quadratic in
, the worst case
complexity of the ACCL algorithm is quadratic in 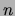 .
Empirically, however, as we show below, we find that the dependence
of
.
Empirically, however, as we show below, we find that the dependence
of 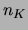 on
on 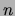 is generally subquadratic. Moreover, random graph
theory implies that if the distribution of the weight values
is the same for all edges, then Kruskal's algorithm should take
time proportional to
is generally subquadratic. Moreover, random graph
theory implies that if the distribution of the weight values
is the same for all edges, then Kruskal's algorithm should take
time proportional to 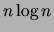 [West 1996]. To verify this
latter result, we conducted a set of Monte Carlo experiments,
in which we ran the Kruskal algorithm on sets of random weights
over domains of dimension up to
[West 1996]. To verify this
latter result, we conducted a set of Monte Carlo experiments,
in which we ran the Kruskal algorithm on sets of random weights
over domains of dimension up to 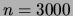 . For each
. For each 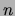 , 1000
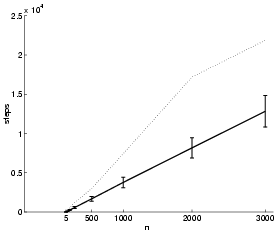
runs were performed. Figure 22 plots the average
and maximum
, 1000
runs were performed. Figure 22 plots the average
and maximum 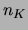 versus
versus 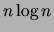 for these experiments. The curve
for the average displays an essentially linear dependence.
for these experiments. The curve
for the average displays an essentially linear dependence.
Figure 22:
The mean (full line), standard
deviation and maximum (dotted line) of the number of steps 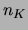 in the Kruskal algorithm over 1000 runs plotted against
in the Kruskal algorithm over 1000 runs plotted against 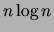 .
.
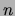 ranges from 5 to 3000. The edge weights were sampled from a
uniform distribution.
ranges from 5 to 3000. The edge weights were sampled from a
uniform distribution.
 |



Next: Memory requirements
Up: The ACCL algorithm
Previous: The algorithm and its
Journal of Machine Learning Research
2000-10-19
