


Next: Comparing mutual information between
Up: The accelerated tree learning
Previous: The accelerated tree learning
The ACCL algorithm
We first present the ACCL algorithm for the case of binary
variables, presenting the extension to general discrete variables
in Section 6.2. For binary variables
we will say that a variable is ``on'' when it takes value 1; otherwise
we say that it is ``off''. Without loss of generality we assume
that a variable is off more times than it is on in the given dataset.
The target distribution 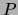 is assumed to be derived from a set of
observations of size
is assumed to be derived from a set of
observations of size 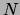 . Let us denote by
. Let us denote by 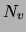 the number of times
variable
the number of times
variable  is on in the dataset and by
is on in the dataset and by 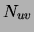 the number of times
variables
the number of times
variables 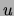 and
and  are simultaneously on. We call each of the latter
events a co-occurrence of
are simultaneously on. We call each of the latter
events a co-occurrence of 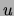 and
and  . The marginal
. The marginal 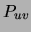 of
of
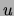 and
and  is given by:
is given by:
All the information about 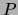 that is necessary for fitting the tree
is summarized in the counts
that is necessary for fitting the tree
is summarized in the counts 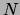 ,
, 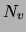 and
and
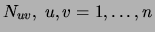 ,
and from now on we will consider
,
and from now on we will consider 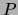 to be represented by these counts.
(It is an easy extension to handle non-integer data, such as when
the data points are ``weighted'' by real numbers).
We now define the notion of sparseness that motivates the ACCL
algorithm. Let us denote by
to be represented by these counts.
(It is an easy extension to handle non-integer data, such as when
the data points are ``weighted'' by real numbers).
We now define the notion of sparseness that motivates the ACCL
algorithm. Let us denote by 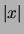 the number of variables that are
on in observation
the number of variables that are
on in observation 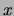 , where
, where
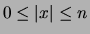 . Define
. Define 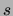 , the
data sparseness
, the
data sparseness
If, for example, the data are documents and the variables represent
words from a vocabulary, then 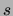 represents the maximum number of
distinct words in a document. The time and memory requirements of
the algorithm that we describe depend on the sparseness
represents the maximum number of
distinct words in a document. The time and memory requirements of
the algorithm that we describe depend on the sparseness 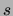 ; the lower
the sparseness, the more efficient the algorithm. Our algorithm will
realize its largest performance gains when
; the lower
the sparseness, the more efficient the algorithm. Our algorithm will
realize its largest performance gains when 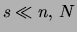 .
Recall that the CHOWLIU algorithm greedily adds edges to a
graph by choosing the edge that currently has the maximal value of mutual
information. The algorithm that we describe involves an efficient
way to rank order mutual information. There are two key aspects
to the algorithm: (1) how to compare mutual information between
non-co-occurring variables, and (2) how to compute co-occurrences
in a list representation.
.
Recall that the CHOWLIU algorithm greedily adds edges to a
graph by choosing the edge that currently has the maximal value of mutual
information. The algorithm that we describe involves an efficient
way to rank order mutual information. There are two key aspects
to the algorithm: (1) how to compare mutual information between
non-co-occurring variables, and (2) how to compute co-occurrences
in a list representation.
Subsections



Next: Comparing mutual information between
Up: The accelerated tree learning
Previous: The accelerated tree learning
Journal of Machine Learning Research
2000-10-19