


Next: Computing co-occurrences
Up: The accelerated tree learning
Previous: Memory requirements
Discrete variables of arbitrary arity
We briefly describe the extension of the ACCL algorithm
to the case of discrete domains in which the variables can take more
than two values.
First we extend the definition of data sparseness: we assume that
for each variable there exists a special value that appears with
higher frequency than all the other values. This value will be denoted
by 0, without loss of generality. For example, in a medical domain,
the value 0 for a variable would represent the ``normal'' value,
whereas the abnormal values of each variable would be designated by
non-zero values. An ``occurrence'' for variable  will be the event
will be the event
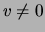 and a ``co-occurrence'' of
and a ``co-occurrence'' of 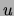 and
and  means that
means that 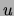 and
and  are
both non-zero for the same data point. We define
are
both non-zero for the same data point. We define 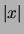 as the number of
non-zero values in observation
as the number of
non-zero values in observation 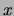 . The sparseness
. The sparseness 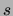 is, as
before, the maximum of
is, as
before, the maximum of 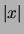 over the data set.
To exploit the high frequency of the zero values we represent
only the occurrences explicitly, creating thereby a compact and
efficient data structure. We obtain performance gains by
presorting mutual information values for non-co-occurring variables.
over the data set.
To exploit the high frequency of the zero values we represent
only the occurrences explicitly, creating thereby a compact and
efficient data structure. We obtain performance gains by
presorting mutual information values for non-co-occurring variables.
Subsections



Next: Computing co-occurrences
Up: The accelerated tree learning
Previous: Memory requirements
Journal of Machine Learning Research
2000-10-19