

Next: Presorting mutual information values
Up: Discrete variables of arbitrary
Previous: Discrete variables of arbitrary
As before, we avoid representing zero values explicitly by
replacing each data point 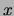 by the list
by the list 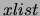 , where
, where
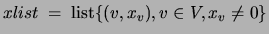 .
A co-occurrence is represented by the quadruple
.
A co-occurrence is represented by the quadruple 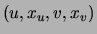 ,
,
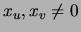 . Instead of one co-occurrence count
. Instead of one co-occurrence count 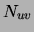 , we
now have a two-way contingency table
, we
now have a two-way contingency table 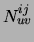 . Each
. Each 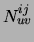 represents the number of data points where
represents the number of data points where
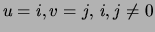 .
Counting and storing co-occurrences can be done in the same
time as before and with a
.
Counting and storing co-occurrences can be done in the same
time as before and with a
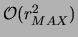 larger amount
of memory, necessitated by the additional need to store the
(non-zero) variable values.
larger amount
of memory, necessitated by the additional need to store the
(non-zero) variable values.
Journal of Machine Learning Research
2000-10-19