


Next: Experiments
Up: Discrete variables of arbitrary
Previous: Computing co-occurrences
Our goal is to presort the mutual information values 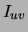 for all
for all
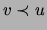 that do not co-occur with
that do not co-occur with 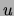 . The following theorem
shows that this can be done exactly as before.
Theorem Let
. The following theorem
shows that this can be done exactly as before.
Theorem Let 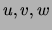 be discrete variables such that
be discrete variables such that 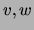 do
not co-occur with
do
not co-occur with 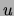 (i.e.
(i.e.
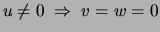 ) in a given
dataset
) in a given
dataset 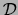 . Let
. Let 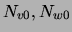 be the number of datapoints for
which
be the number of datapoints for
which  and
and  respectively, and let
respectively, and let 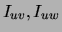 be the
respective empirical mutual information values based on the sample
be the
respective empirical mutual information values based on the sample
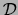 . Then
. Then
with equality only if 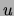 is identically 0.
The proof of the theorem is given in the Appendix. The implication
of this theorem is that the ACCL algorithm can be extended to
variables taking more than two values by making only one (minor)
modification: the replacement of the scalar counts
is identically 0.
The proof of the theorem is given in the Appendix. The implication
of this theorem is that the ACCL algorithm can be extended to
variables taking more than two values by making only one (minor)
modification: the replacement of the scalar counts 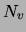 and
and 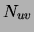 by the vectors
by the vectors
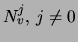 and, respectively, the contingency
tables
and, respectively, the contingency
tables
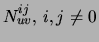 .
.
Figure 23:
Running time for the ACCL (full line)
and (dotted line) CHOWLIU algorithms versus number of vertices 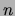 for different values of the sparseness
for different values of the sparseness 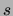 .
.
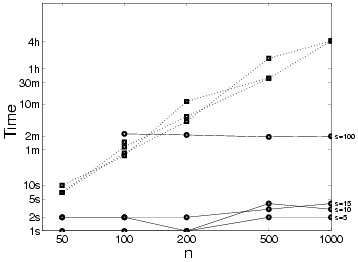 |
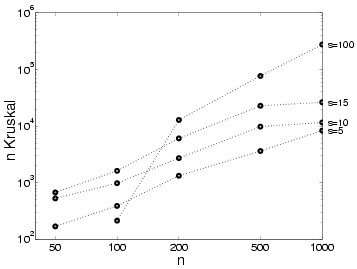
Figure 24:
Number of steps of the Kruskal algorithm 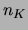 versus domain size
versus domain size 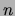 measured for the ACCL algorithm for different values of
measured for the ACCL algorithm for different values of 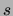 .
.
 |



Next: Experiments
Up: Discrete variables of arbitrary
Previous: Computing co-occurrences
Journal of Machine Learning Research
2000-10-19

