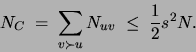

Next: The algorithm and its
Up: The ACCL algorithm
Previous: Comparing mutual information between
Let
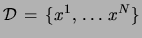 be a set of observations
over
be a set of observations
over 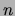 binary variables. If
binary variables. If  it is efficient to represent each
observation in
it is efficient to represent each
observation in 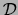 as a list of the variables that are on in
the respective observation. Thus, data point
as a list of the variables that are on in
the respective observation. Thus, data point
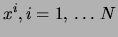 will be represented by the list
will be represented by the list
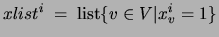 . The space required by the lists is no more than
. The space required by the lists is no more than 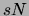 and
is much smaller than the space required by the binary vector
representation of the same data (i.e.,
and
is much smaller than the space required by the binary vector
representation of the same data (i.e., 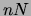 ).
Note, moreover, that the total number
).
Note, moreover, that the total number 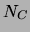 of co-occurrences in
the dataset
of co-occurrences in
the dataset 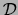 is
is
For the variables that co-occur with 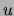 , a set of co-occurrence
lists
, a set of co-occurrence
lists 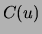 is created. Each
is created. Each 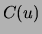 contains records
contains records
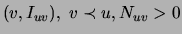 and is sorted by
decreasing
and is sorted by
decreasing 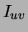 . To represent the lists
. To represent the lists 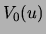 (that
contain many elements) we use their ``complements''
(that
contain many elements) we use their ``complements''
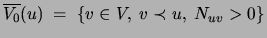 .
It can be shown [Meila-Predoviciu 1999] that the computation of the co-occurrence
counts and the construction of the lists
.
It can be shown [Meila-Predoviciu 1999] that the computation of the co-occurrence
counts and the construction of the lists 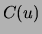 and
and
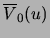 ,
for all
,
for all 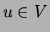 , takes an amount of time proportional to the number
of co-occurrences
, takes an amount of time proportional to the number
of co-occurrences 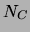 , up to a logarithmic factor:
, up to a logarithmic factor:
Comparing this value with
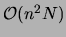 , which is the time to compute
, which is the time to compute
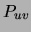 in the CHOWLIU algorithm, we see that the present method
replaces the dimension of the domain
in the CHOWLIU algorithm, we see that the present method
replaces the dimension of the domain 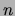 by
by 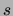 . The memory requirements
for the lists are also at most proportional to
. The memory requirements
for the lists are also at most proportional to 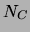 , hence
, hence
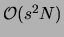 .
.


Next: The algorithm and its
Up: The ACCL algorithm
Previous: Comparing mutual information between
Journal of Machine Learning Research
2000-10-19