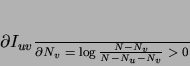

Next: Computing co-occurrences in a
Up: The ACCL algorithm
Previous: The ACCL algorithm
Let us focus on the pairs  that do not co-occur, i.e., for
which
that do not co-occur, i.e., for
which 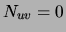 . For such a pair, the mutual information
. For such a pair, the mutual information 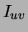 is a
function of
is a
function of 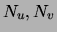 and
and 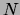 . Let us analyze the variation of the mutual
information with respect to
. Let us analyze the variation of the mutual
information with respect to 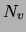 by taking the corresponding partial
derivative:
by taking the corresponding partial
derivative:
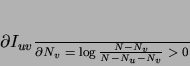 |
(11) |
This result implies that for a given variable 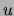 and any two variables
and any two variables
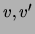 for which
for which
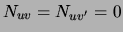 we have:
we have:
This observation allows us to partially sort the mutual information values
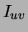 for non-co-occurring pairs
for non-co-occurring pairs 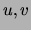 , without computing
them. First, we have to sort all the variables by their number of
occurrences
, without computing
them. First, we have to sort all the variables by their number of
occurrences 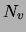 . We store the result in a list
. We store the result in a list 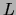 . This gives a
total ordering ``
. This gives a
total ordering ``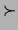 '' for the variables in
'' for the variables in 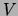 :
:
For each 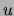 , we define the list of variables following
, we define the list of variables following 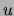 in the
ordering ``
in the
ordering ``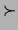 '' and not co-occurring with it:
'' and not co-occurring with it:
This list is sorted by decreasing 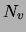 and therefore,
implicitly, by decreasing
and therefore,
implicitly, by decreasing 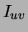 . Since the data are sparse, most
pairs of variables do not co-occur. Therefore, by creating the lists
. Since the data are sparse, most
pairs of variables do not co-occur. Therefore, by creating the lists
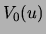 , a large number of values of the mutual information are partially
sorted. Before showing how to use this construction, let us examine an
efficient way of computing the
, a large number of values of the mutual information are partially
sorted. Before showing how to use this construction, let us examine an
efficient way of computing the 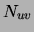 counts when the data are
sparse.
counts when the data are
sparse.
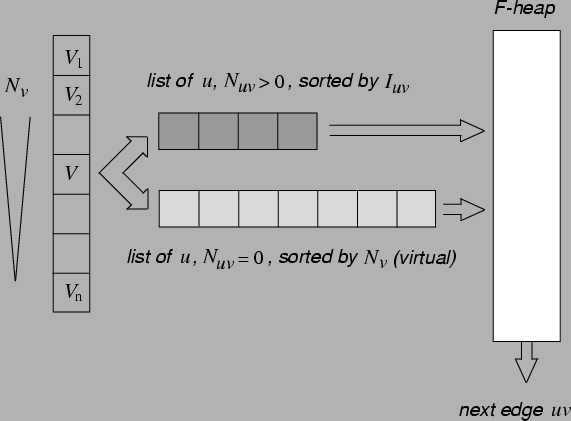
Figure 20:
The data structure that supplies the next candidate edge. Vertically
on the left are the variables, sorted by decreasing 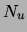 . For a
given
. For a
given 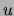 , there are two lists:
, there are two lists: 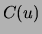 , sorted by decreasing
, sorted by decreasing 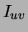 and (the virtual list)
and (the virtual list) 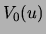 , sorted by decreasing
, sorted by decreasing 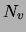 . The
maximum of the two first elements of these lists is inserted into
an Fibonacci heap. The overall maximum of
. The
maximum of the two first elements of these lists is inserted into
an Fibonacci heap. The overall maximum of 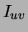 can then be extracted as
the maximum of the Fibonacci heap.
can then be extracted as
the maximum of the Fibonacci heap.
 |


Next: Computing co-occurrences in a
Up: The ACCL algorithm
Previous: The ACCL algorithm
Journal of Machine Learning Research
2000-10-19