


Next: The accelerated tree learning
Up: Classification with mixtures of
Previous: The SPLICE dataset: Structure
The SPLICE dataset: Feature selection
Let us examine the single tree classifier that was used for the
SPLICE data set more closely. According to the Markov properties
of the tree distribution, the probability of the class variables
depends only on its neighbors, that is, on the variables to which the
class variable is connected by tree edges. Hence, a tree acts as an
implicit variable selector for classification: only the variables
adjacent to the queried variable (this set of variables is called the
Markov blanket; pearl:88) are relevant for determining its
probability distribution. This property also explains the observed
preservation of the accuracy of the tree classifier when the size of the
training set decreases: out of the 60 variables, only 18 are relevant to
the class; moreover, the dependence is parametrized as 18 independent pairwise
probability tables  . Such parameters can be fit accurately
from relatively few examples. Hence, as long as the training set
contains enough data to establish the correct dependency structure,
the classification accuracy will degrade slowly with the decrease in
the size of the data set.
This explanation helps to understand the superiority of the tree
classifier over the models in DELVE: only a small subset of variables
are relevant for classification. The tree finds them correctly. A
classifier that is not able to perform feature selection reasonably
well will be hindered by the remaining irrelevant variables,
especially if the training set is small.
For a given Markov blanket, the tree classifies in the same
way as a naive Bayes model with the Markov blanket variables as
inputs. Note also that the naive Bayes model itself has a built-in
feature selector: if one of the input variables
. Such parameters can be fit accurately
from relatively few examples. Hence, as long as the training set
contains enough data to establish the correct dependency structure,
the classification accuracy will degrade slowly with the decrease in
the size of the data set.
This explanation helps to understand the superiority of the tree
classifier over the models in DELVE: only a small subset of variables
are relevant for classification. The tree finds them correctly. A
classifier that is not able to perform feature selection reasonably
well will be hindered by the remaining irrelevant variables,
especially if the training set is small.
For a given Markov blanket, the tree classifies in the same
way as a naive Bayes model with the Markov blanket variables as
inputs. Note also that the naive Bayes model itself has a built-in
feature selector: if one of the input variables  is not relevant to
the class, the distributions
is not relevant to
the class, the distributions 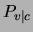 will be roughly the same for
all values of
will be roughly the same for
all values of 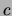 . Consequently, in the posterior
. Consequently, in the posterior 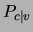 that
serves for classification, the factors corresponding to
that
serves for classification, the factors corresponding to  will
simplify and thus
will
simplify and thus  will have little influence on the
classification. This may explain why the naive Bayes model also performs
well on the SPLICE classification task. Notice however that the
variable selection mechanisms implemented by the tree classifier and
the naive Bayes classifier are not the same.
To verify that indeed the single tree classifier acts like a feature
selector, we performed the following experiment, again using the
SPLICE data. We augmented the variable set with another 60 variables,
each taking 4 values with randomly and independently assigned
probabilities. The rest of the experimental conditions (training set,
test set and number of random restarts) were identical to the first
SPLICE experiment. We fit a set of models with
will have little influence on the
classification. This may explain why the naive Bayes model also performs
well on the SPLICE classification task. Notice however that the
variable selection mechanisms implemented by the tree classifier and
the naive Bayes classifier are not the same.
To verify that indeed the single tree classifier acts like a feature
selector, we performed the following experiment, again using the
SPLICE data. We augmented the variable set with another 60 variables,
each taking 4 values with randomly and independently assigned
probabilities. The rest of the experimental conditions (training set,
test set and number of random restarts) were identical to the first
SPLICE experiment. We fit a set of models with  , a small
, a small
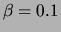 and no smoothing. The structure of the new models,
in the form of a cumulative adjacency matrix, is shown in
Figure 19. We see that the structure over the
original 61 variables is unchanged and stable; the 60 noise
variables connect in a random uniform patterns to the original
variables and among each other. As expected after examining the
structure, the classification performance of the new trees is not
affected by the newly introduced variables: in fact the average
accuracy of the trees over 121 variables is 95.8%, 0.1%
higher than the accuracy of the original trees.
and no smoothing. The structure of the new models,
in the form of a cumulative adjacency matrix, is shown in
Figure 19. We see that the structure over the
original 61 variables is unchanged and stable; the 60 noise
variables connect in a random uniform patterns to the original
variables and among each other. As expected after examining the
structure, the classification performance of the new trees is not
affected by the newly introduced variables: in fact the average
accuracy of the trees over 121 variables is 95.8%, 0.1%
higher than the accuracy of the original trees.



Next: The accelerated tree learning
Up: Classification with mixtures of
Previous: The SPLICE dataset: Structure
Journal of Machine Learning Research
2000-10-19