![]()
![]()
![]()
Next: Introduction
Journal of Machine Learning Research (3) 2002 145-174 Submitted 10/01; Revised 1/02; Published 8/02
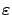 -MDPs: Learning in Varying Environments
-MDPs: Learning in Varying Environments
István Szita szityu@cs.elte.hu
Bálint Takács deim@inf.elte.hu
András Lőrincz lorincz@inf.elte.hu
Department of Information Systems, Eötvös Loránd University
Pázmány Péter sétány 1/C
Budapest, Hungary H-1117
Editor: Sridhar Mahadevan
Abstract
In this paper ![]() -MDP-models are introduced and convergence
theorems are proven using the generalized MDP framework of Szepesvári and
Littman. Using this model family, we show that Q-learning is capable of finding
near-optimal policies in varying environments. The potential of this new family
of MDP models is illustrated via a reinforcement learning algorithm called event-learning
which separates the optimization of decision making from the controller. We
show that event-learning augmented by a particular controller, which gives rise
to an
-MDP-models are introduced and convergence
theorems are proven using the generalized MDP framework of Szepesvári and
Littman. Using this model family, we show that Q-learning is capable of finding
near-optimal policies in varying environments. The potential of this new family
of MDP models is illustrated via a reinforcement learning algorithm called event-learning
which separates the optimization of decision making from the controller. We
show that event-learning augmented by a particular controller, which gives rise
to an ![]() -MDP, enables near optimal performance even
if considerable and sudden changes may occur in the environment. Illustrations
are provided on the two-segment pendulum problem.
-MDP, enables near optimal performance even
if considerable and sudden changes may occur in the environment. Illustrations
are provided on the two-segment pendulum problem.
![]()
- Sampling from Near-identical Distributions
- Stochastic Processes with Non-diminishing Perturbations
- Event-learning
with a background controller can be formulated as an
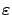 -MDP
-MDP
- Bibliography