Formalizing Event-Learning in the Generalized $\varepsilon$-MDP Framework

In most applications we cannot assume that a time-independent optimal controller policy exists. To the contrary, we may have to allow the controller policy to adapt over time. In this case, we may try to require asymptotic near-optimality. This is a more realistic requirement: in many cases it can be fulfilled, e.g., by learning an approximate inverse dynamics [Fomin et al.(1997)] in parallel with E-learning. Or alternatively, the controller policy itself may be subject to reinforcement learning (with a finer state space resolution), thus defining a modular hierarchy. Another attractive solution is the application of a robust controller like the SDS controller [Szepesvári and Lorincz(1997)], which is proven to be asymptotically near-optimal. Furthermore, the SDS controller has short adaptation time, and is robust against perturbations of the environment.

As a consequence of the varying environment (recall that from the viewpoint of E-learning, the controller policy is the part of the environment), we cannot prove convergence any more. But we may apply Theorem 3.3 to show that there exists an iteration which still finds a near-optimal event-value function. To this end, we have to re-formulate E-learning in the generalized $\varepsilon$-MDP framework.

One can define a generalized $\varepsilon$-MDP such that its generalized Q-learning algorithm is identical to our E-learning algorithm: Let the state set and the transition probabilities of the E-learning algorithm be defined by $X$ and $P$, respectively. In the new generalized $\varepsilon$-MDP the set of states will also be $X$, and since an action of the learning agent is selecting a new desired state, the set of actions $A$ is also equal to $X$. (Note that because of this assignment, the generalized Q-value function of this model will be exactly our event-value function $E$.) The definition of the reward function $R$ is evident: $R(x,y^d,y)$ gives the reward for arriving at $y$ from $x$, when the desired state was $y^d$. Let $({\textstyle\bigotimes}_t E)(x) = \max_{y^d} E(x,y^d)$, independently of $t$, and let $({\textstyle\bigoplus}_t S)(x,y^d) = \sum_y p_t(y \vert x,y^d) S(x,y^d,y)$, where $p_t(y\vert x,y^d) = \sum_u \pi_t^A(x,y^d,u) P(x, u, y)$ (see Equation 9).

Finally, we assign the operators ${\textstyle\bigoplus}$ and ${\textstyle\bigotimes}$ as $({\textstyle\bigotimes} E)(x) = \max_{y^d} E(x,y^d)$ and $({\textstyle\bigoplus}S)(x,y^d) = \sum_y \sum_u \pi^A(x,y^d,u) P(x, u, y) S(x,y^d,y)$.

The generalized Q-learning algorithm of this model uses the iteration

$$E_{t+1}(s_t,s_{t+1}^d) = (1-\alpha_t(s_t,s_{t+1}^d)) E_{t}(s_t,s_... ...pha_t(s_t,s_{t+1}^d) \left( r_t + \gamma \max_{s^d} E_{t}(s_{t+1},s^d) \right).$$

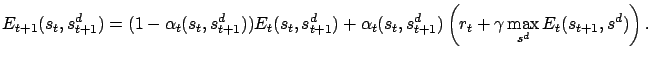This is identical to the iteration defined by [Lorincz et al.(2002)]. Here $s_t$ is the sequence containing the realized states at time instant t and $s^d_{t+1}$ is the sequence containing the desired state for time instant $t+1$.