

Next: The Convergence of the
Up: Convergence Theorems in Generalized
Previous: Convergence Theorems in Generalized
Let 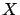 be an arbitrary state-space and denote by
be an arbitrary state-space and denote by
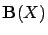 the set of value functions over
the set of value functions over 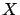 (i.e., the set of bounded
(i.e., the set of bounded
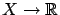 functions), and let
functions), and let
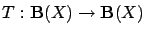 be an arbitrary contraction mapping with (unique)
fixed point
be an arbitrary contraction mapping with (unique)
fixed point 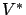 .
.
Let
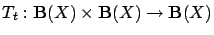 be
a sequence of stochastic operators. The second argument of
be
a sequence of stochastic operators. The second argument of 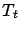 is intended to modify the first one, in order to get a better
approximation of
is intended to modify the first one, in order to get a better
approximation of 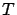 . Formally, let
. Formally, let 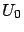 be an arbitrary value
function and let
be an arbitrary value
function and let
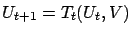 .
. 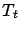 is said to
approximate
is said to
approximate 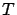 at
at 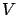 with probability one over
with probability one over 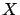 , if
, if
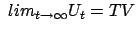 uniformly over
uniformly over 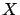 .
.
Theorem A.1 (Szepesvári and Littman)
Let the sequence of random operators
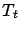
approximate
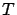
at
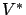
with probability one uniformly over
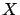
. Let
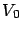
be an
arbitrary value function, and define
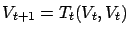
. If
there exist functions
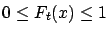
and
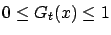
satisfying the conditions below with probability one, then
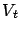
converges to
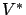
with probability one uniformly over
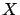
:
- for all
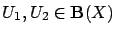 and all
and all 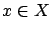 ,
,
- for all
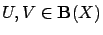 and all
and all 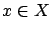 ,
,
- for all
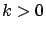 ,
,
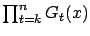 converges to zero uniformly in
converges to zero uniformly in 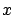 as
as 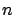 increases; and,
increases; and,
- there exists
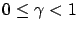 such that for all
such that for all 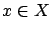 and large enough
and large enough 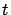 ,
,
The proof can be found in [Szepesvári and Littman(1996)]. We cite
here the lemma, which is the base of the proof, since our
generalization concerns this lemma.
Lemma A.2
Let
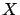
be an arbitrary set,
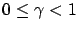
and consider the
sequence
where
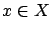
,
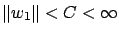
with probability one for
some
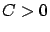
,
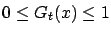
and
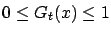
for all
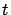
, and
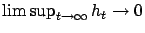
w.p.1. Assume that for
all
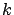
,
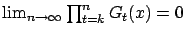
uniformly in
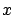
w.p.1 and
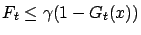
w.p.1. Then
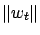
converges to 0 w.p.1 as well.


Next: The Convergence of the
Up: Convergence Theorems in Generalized
Previous: Convergence Theorems in Generalized
![]() be an arbitrary state-space and denote by
be an arbitrary state-space and denote by
![]() the set of value functions over
the set of value functions over ![]() (i.e., the set of bounded
(i.e., the set of bounded
![]() functions), and let
functions), and let
![]() be an arbitrary contraction mapping with (unique)
fixed point
be an arbitrary contraction mapping with (unique)
fixed point ![]() .
.
![]() be
a sequence of stochastic operators. The second argument of
be
a sequence of stochastic operators. The second argument of ![]() is intended to modify the first one, in order to get a better
approximation of
is intended to modify the first one, in order to get a better
approximation of ![]() . Formally, let
. Formally, let ![]() be an arbitrary value
function and let
be an arbitrary value
function and let
![]() .
. ![]() is said to
approximate
is said to
approximate ![]() at
at ![]() with probability one over
with probability one over ![]() , if
, if
![]() uniformly over
uniformly over ![]() .
.