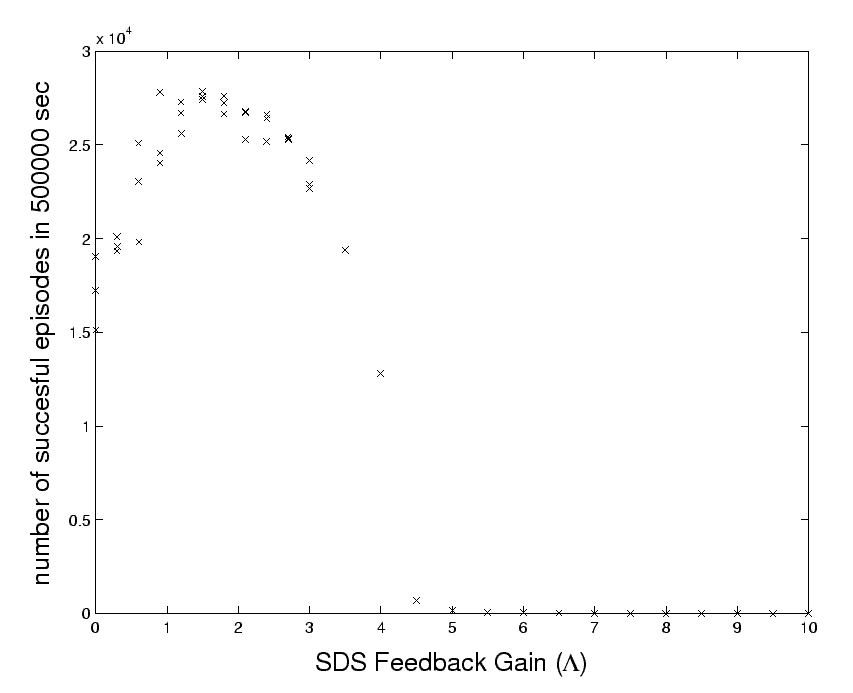
By Corollary 4.3, we can expect that the time
needed for convergence decreases by increasing the gain factor
![]() . Indeed, Figure 6 shows that an optimal
. Indeed, Figure 6 shows that an optimal
![]() exists. At higher gain factors, the discretization
introduces instabilities: The SDS ``overshoots'' within
discretization domains. Therefore performance quickly deteriorates
for large
exists. At higher gain factors, the discretization
introduces instabilities: The SDS ``overshoots'' within
discretization domains. Therefore performance quickly deteriorates
for large ![]() values. Finer discretization and/or more
frequent observations are needed to improve performance: for
larger
values. Finer discretization and/or more
frequent observations are needed to improve performance: for
larger ![]() values the update rate needs to be increased.
values the update rate needs to be increased.
|