Proof.
We will prove that for each
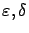
there exists an
index
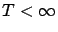
such that
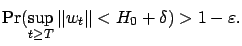 |
(15) |
Fix
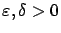
arbitrarily. Furthermore fix a sequence
of
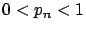
numbers (
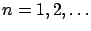
) to be chosen later.
Let
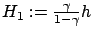 and
and
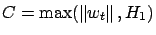 . Then
. Then
Thus, we have that
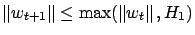 . Now
define
. Now
define
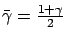 . Since
. Since
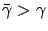 ,
,
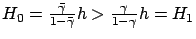 . Consequently, if
. Consequently, if
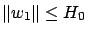 , then
, then
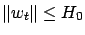 holds for all
holds for all 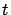 , as well. From
now on, we will assume that
, as well. From
now on, we will assume that
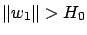 .
.
Let
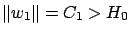 . Since
. Since
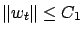 , the
process
, the
process
with
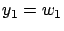
estimates the process
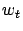
from above:
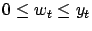
holds for all
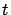
. The process
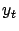
converges to
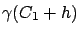
w.p.1 uniformly over
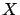
, so
w.p.1. Since
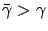
, there exists an index
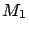
,
for which if
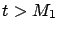
then
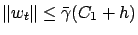
with
probability
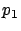
. The proof goes on by induction: assume that up
to some index
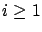
we have found indices
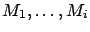
such that when
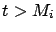
then
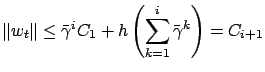 |
(16) |
holds with probability
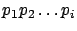
. Now let us restrict
ourselves to those events for which inequality (
16)
holds. Then we see that the process
bounds
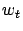
from above from the index
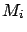
. The process
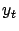
converges to
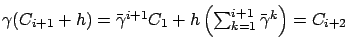
w.p.1 uniformly
over
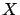
, so the above argument can be repeated to obtain an index
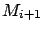
such that (
16) holds for
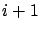
with
probability
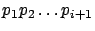
.
Since
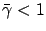 ,
,
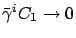 and
and
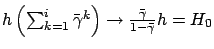 . So there exists an index
. So there exists an index
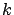 for which
for which
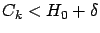 . Then inequality (15)
can be satisfied by setting
. Then inequality (15)
can be satisfied by setting
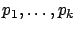 so that
so that
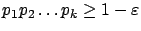 holds and letting
holds and letting 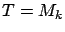 .
.

![]() and
and
![]() . Then
. Then
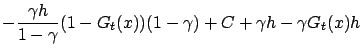
![]() . Now
define
. Now
define
![]() . Since
. Since
![]() ,
,
![]() . Consequently, if
. Consequently, if
![]() , then
, then
![]() holds for all
holds for all ![]() , as well. From
now on, we will assume that
, as well. From
now on, we will assume that
![]() .
.
![]() . Since
. Since
![]() , the
process
, the
process
![]() ,
,
![]() and
and
![]() . So there exists an index
. So there exists an index
![]() for which
for which
![]() . Then inequality (15)
can be satisfied by setting
. Then inequality (15)
can be satisfied by setting
![]() so that
so that
![]() holds and letting
holds and letting ![]() .
.
![]()