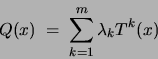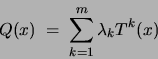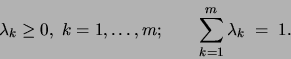Next: Marginalization, inference and sampling
Up: Learning with Mixtures of
Previous: Learning of tree distributions
Mixtures of trees
We define a mixture-of-trees (MT) model to be a distribution of
the form:
with
The tree distributions 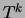 are the mixture components and
are the mixture components and
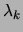 are called mixture coefficients. A mixture of trees
can be viewed as containing an unobserved choice variable
are called mixture coefficients. A mixture of trees
can be viewed as containing an unobserved choice variable 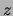 ,
which takes value
,
which takes value
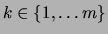 with probability
with probability 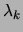 .
Conditioned on the value of
.
Conditioned on the value of 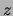 , the distribution of the observed
variables
, the distribution of the observed
variables 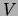 is a tree. The
is a tree. The 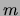 trees may have different structures
and different parameters. In Figure 1, for example,
we have a mixture of trees with
trees may have different structures
and different parameters. In Figure 1, for example,
we have a mixture of trees with  and
and  .
Note that because of the varying structure of the component trees, a
mixture of trees is neither a Bayesian network nor a Markov random field.
Let us adopt the notation
.
Note that because of the varying structure of the component trees, a
mixture of trees is neither a Bayesian network nor a Markov random field.
Let us adopt the notation
for ``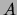 is independent of
is independent of 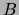 given
given 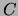 under distribution
under distribution
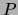 ''. If for some (all)
''. If for some (all)
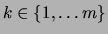 we have
we have
this will not imply that
On the other hand, a mixture of trees is capable of representing
dependency structures that are conditioned on the value of a
variable (the choice variable), something that a usual Bayesian
network or Markov random field cannot do. Situations where such a model is
potentially useful abound in real life: Consider for example bitmaps
of handwritten digits. Such images obviously contain many dependencies
between pixels; however, the pattern of these dependencies will vary
across digits. Imagine a medical database recording the body weight
and other data for each patient. The body weight could be a function
of age and height for a healthy person, but it would depend on other
conditions if the patient suffered from a disease or were an athlete.
If, in a situation like the ones mentioned above, conditioning on one
variable produces a dependency structure characterized by sparse,
acyclic pairwise dependencies, then a mixture of trees may provide
a good model of the domain.
If we constrain all of the trees in the mixture to have the same structure
we obtain a mixture of trees with shared structure (MTSS;
see Figure 4).
Figure 4:
A mixture of trees with shared structure (MTSS) represented as a Bayes net (a) and as a Markov random field (b).
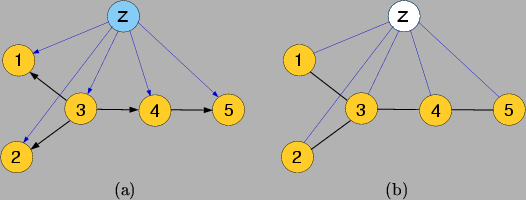 |
In the case of the MTSS, if for some (all)
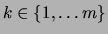
then
In addition, a MTSS can be represented as a Bayesian network
(Figure 4,a), as a Markov random field
(Figure 4,b) and as a chain graph
(Figure 5). Chain graphs were introduced by
Lauritzen:96; they represent a superclass of both Bayesian
networks and Markov random fields. A chain graph contains both
directed and undirected edges.
Figure 5:
A MTSS represented as a chain graph. The double boxes enclose the undirected blocks of the chain graph.
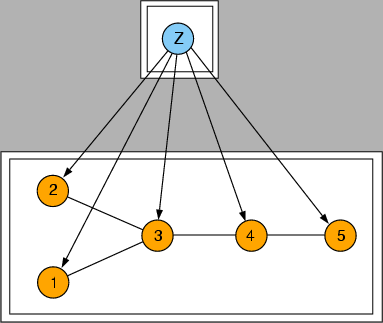 |
While we generally consider problems in which the choice variable
is hidden (i.e., unobserved), it is also possible to utilize both the
MT and the MTSS frameworks in which the choice variable is observed.
Such models, which--as we discuss in Section 1.1--have
been studied previously by friedman:97 and friedman:98a,
will be referred to generically as mixtures with observed choice
variable. Unless stated otherwise, it will be assumed that the
choice variable is hidden.
Subsections



Next: Marginalization, inference and sampling
Up: Learning with Mixtures of
Previous: Learning of tree distributions
Journal of Machine Learning Research
2000-10-19