


Next: Tree distributions
Up: Introduction
Previous: Introduction
Related work
The MT model can be used both in the classification setting and
the density estimation setting, and it makes contact with
different strands of previous literature in these two guises.
In the classification setting, the MT model builds on the seminal
work on tree-based classifiers by [Chow, Liu 1968], and
on recent extensions due to friedman:97 and friedman:98a.
Chow and Liu proposed to solve 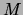 -way classification problems by
fitting a separate tree to the observed variables in each of the
-way classification problems by
fitting a separate tree to the observed variables in each of the
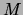 classes, and classifying a new data point by choosing the class
having maximum class-conditional probability under the corresponding tree
model. Friedman et al. took as their point of
departure the Naive Bayes model, which can be viewed as a graphical
model in which an explicit class node has directed edges to an
otherwise disconnected set of nodes representing the input variables
(i.e., attributes). Introducing additional edges between the input
variables yields the Tree Augmented Naive Bayes (TANB) classifier
[Friedman, Geiger, Goldszmidt
1997,Geiger 1992]. These authors also considered a
less constrained model in which different patterns of edges were
allowed for each value of the class node--this is formally
identical to the Chow and Liu proposal.
If the choice variable of the MT model is identified with the
class label then the MT model is identical to the Chow and Liu
approach (in the classification setting). However, we do not
necessarily wish to identify the choice variable with the class
label, and, indeed, in our experiments on classification we treat
the class label as simply another input variable. This yields
a more discriminative approach to classification in which all of
the training data are pooled for the purposes of training the model
(Section 5, MJ:nips98).
The choice variable remains hidden, yielding a mixture model for
each class. This is similar in spirit to the ``mixture discriminant
analysis'' model of hastie:96, where a mixture of
Gaussians is used for each class in a multiway
classification problem.
In the setting of density estimation, clustering and compression
problems, the MT model makes contact with the large and active
literature on mixture modeling. Let us briefly review some of the
most salient connections. The Auto-Class model [Cheeseman, Stutz 1995] is
a mixture of factorial distributions (MF), and its excellent
cost/performance ratio motivates the MT model in much the same way as
the Naive Bayes model motivates the TANB model in the classification
setting. (A factorial distribution is a product of factors
each of which depends on exactly one variable). tirri:97
study a MF in which a hidden variable is used for classification;
this approach was extended by monti:98. The idea of learning
tractable but simple belief networks and superimposing a mixture to account
for the remaining dependencies was developed independently of our work
by thiesson:97, who studied mixtures of Gaussian
belief networks. Their work interleaves EM parameter search with Bayesian
model search in a heuristic but general algorithm.
classes, and classifying a new data point by choosing the class
having maximum class-conditional probability under the corresponding tree
model. Friedman et al. took as their point of
departure the Naive Bayes model, which can be viewed as a graphical
model in which an explicit class node has directed edges to an
otherwise disconnected set of nodes representing the input variables
(i.e., attributes). Introducing additional edges between the input
variables yields the Tree Augmented Naive Bayes (TANB) classifier
[Friedman, Geiger, Goldszmidt
1997,Geiger 1992]. These authors also considered a
less constrained model in which different patterns of edges were
allowed for each value of the class node--this is formally
identical to the Chow and Liu proposal.
If the choice variable of the MT model is identified with the
class label then the MT model is identical to the Chow and Liu
approach (in the classification setting). However, we do not
necessarily wish to identify the choice variable with the class
label, and, indeed, in our experiments on classification we treat
the class label as simply another input variable. This yields
a more discriminative approach to classification in which all of
the training data are pooled for the purposes of training the model
(Section 5, MJ:nips98).
The choice variable remains hidden, yielding a mixture model for
each class. This is similar in spirit to the ``mixture discriminant
analysis'' model of hastie:96, where a mixture of
Gaussians is used for each class in a multiway
classification problem.
In the setting of density estimation, clustering and compression
problems, the MT model makes contact with the large and active
literature on mixture modeling. Let us briefly review some of the
most salient connections. The Auto-Class model [Cheeseman, Stutz 1995] is
a mixture of factorial distributions (MF), and its excellent
cost/performance ratio motivates the MT model in much the same way as
the Naive Bayes model motivates the TANB model in the classification
setting. (A factorial distribution is a product of factors
each of which depends on exactly one variable). tirri:97
study a MF in which a hidden variable is used for classification;
this approach was extended by monti:98. The idea of learning
tractable but simple belief networks and superimposing a mixture to account
for the remaining dependencies was developed independently of our work
by thiesson:97, who studied mixtures of Gaussian
belief networks. Their work interleaves EM parameter search with Bayesian
model search in a heuristic but general algorithm.



Next: Tree distributions
Up: Introduction
Previous: Introduction
Journal of Machine Learning Research
2000-10-19