

Next: Related work
Up: Learning with Mixtures of
Previous: Learning with Mixtures of
Introduction
Probabilistic inference has become a core technology in AI,
largely due to developments in graph-theoretic methods for the
representation and manipulation of complex probability
distributions [Pearl 1988]. Whether in their guise as
directed graphs (Bayesian networks) or as undirected graphs (Markov
random fields), probabilistic graphical models have a number
of virtues as representations of uncertainty and as inference engines.
Graphical models allow a separation between qualitative, structural
aspects of uncertain knowledge and the quantitative, parametric aspects
of uncertainty--the former represented via patterns of edges in
the graph and the latter represented as numerical values associated
with subsets of nodes in the graph. This separation is often found
to be natural by domain experts, taming some of the problems associated
with structuring, interpreting, and troubleshooting the model.
Even more importantly, the graph-theoretic framework has allowed
for the development of general inference algorithms, which in
many cases provide orders of magnitude speedups over brute-force
methods [Cowell, Dawid, Lauritzen,
Spiegelhalter 1999,Shafer, Shenoy 1990].
These virtues have not gone unnoticed by researchers interested in
machine learning, and graphical models are being widely explored as the
underlying architectures in systems for classification, prediction and
density estimation [Bishop 1999,Friedman, Geiger, Goldszmidt
1997,Heckerman, Geiger, Chickering
1995,Hinton, Dayan, Frey, Neal
1995,Friedman, Getoor, Koller, Pfeffer
1996,Monti,
Cooper 1998,Saul, Jordan 1999].
Indeed, it is possible to view a wide variety of classical machine learning
architectures as instances of graphical models, and the graphical model
framework provides a natural design procedure for exploring architectural
variations on classical themes [Buntine 1996,Smyth, Heckerman, Jordan
1997].
As in many machine learning problems, the problem of learning a
graphical model from data can be divided into the problem of
parameter learning and the problem of structure
learning. Much progress has been made on the former problem,
much of it cast within the framework of the expectation-maximization
(EM) algorithm [Lauritzen 1995]. The EM algorithm essentially
runs a probabilistic inference algorithm as a subroutine to
compute the ``expected sufficient statistics'' for the data,
reducing the parameter learning problem to a decoupled set of local
statistical estimation problems at each node of the graph. This
link between probabilistic inference and parameter learning is an
important one, allowing developments in efficient inference to
have immediate impact on research on learning algorithms.
The problem of learning the structure of a graph from data is
significantly harder. In practice, most structure
learning methods are heuristic methods that perform local
search by starting with a given graph and improving it by
adding or deleting one edge at a time [Heckerman, Geiger, Chickering
1995,Cooper, Herskovits 1992].
There is an important special case in which both parameter learning
and structure learning are tractable, namely the case of graphical
models in the form of a tree distribution. As shown by
[Chow, Liu 1968], the tree distribution that maximizes the
likelihood of a set of observations on 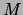 nodes--as well as the
parameters of the tree--can be found in time quadratic in the number
of variables in the domain. This algorithm is known as the Chow-Liu
algorithm.
Trees also have the virtue that probabilistic inference is guaranteed
to be efficient, and indeed historically the earliest research in
AI on efficient inference focused on trees [Pearl 1988].
Later research extended this early work by first considering
general singly-connected graphs [Pearl 1988], and then
considering graphs with arbitrary (acylic) patterns of
connectivity [Cowell, Dawid, Lauritzen,
Spiegelhalter 1999]. This line of research has
provided one useful ``upgrade path'' from tree distributions to the
complex Bayesian and Markov networks currently being studied.
In this paper we consider an alternative upgrade path.
Inspired by the success of mixture models in providing
simple, effective generalizations of classical methods in many simpler
density estimation settings [MacLachlan, Bashford 1988], we consider
a generalization of tree distributions known as the
mixtures-of-trees (MT) model.
As suggested in Figure 1,
nodes--as well as the
parameters of the tree--can be found in time quadratic in the number
of variables in the domain. This algorithm is known as the Chow-Liu
algorithm.
Trees also have the virtue that probabilistic inference is guaranteed
to be efficient, and indeed historically the earliest research in
AI on efficient inference focused on trees [Pearl 1988].
Later research extended this early work by first considering
general singly-connected graphs [Pearl 1988], and then
considering graphs with arbitrary (acylic) patterns of
connectivity [Cowell, Dawid, Lauritzen,
Spiegelhalter 1999]. This line of research has
provided one useful ``upgrade path'' from tree distributions to the
complex Bayesian and Markov networks currently being studied.
In this paper we consider an alternative upgrade path.
Inspired by the success of mixture models in providing
simple, effective generalizations of classical methods in many simpler
density estimation settings [MacLachlan, Bashford 1988], we consider
a generalization of tree distributions known as the
mixtures-of-trees (MT) model.
As suggested in Figure 1,
Figure 1:
A mixture of trees over a domain
consisting of random variables
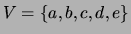 , where
, where 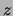 is a hidden choice variable. Conditional on the value
of
is a hidden choice variable. Conditional on the value
of 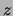 , the dependency structure is a tree. A detailed presentation of the
mixture-of-trees model is provided in Section 3.
, the dependency structure is a tree. A detailed presentation of the
mixture-of-trees model is provided in Section 3.
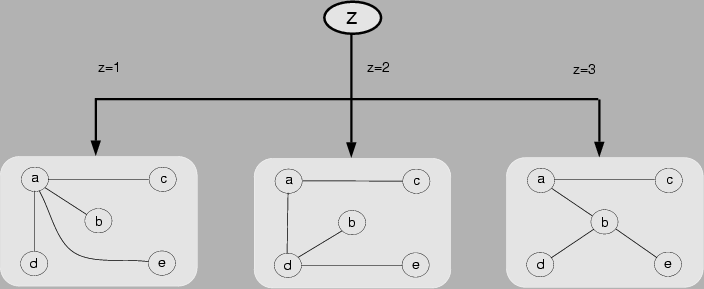 |
the MT model involves the probabilistic mixture of a set of graphical
components, each of which is a tree. In this paper we describe
likelihood-based algorithms for learning the parameters and
structure of such models.
One can also consider probabilistic mixtures of more general graphical
models; indeed, the general case is the Bayesian multinet
introduced by Geiger+Heckerman:96.
The Bayesian multinet is a mixture model in which each mixture
component is an arbitrary graphical model. The advantage of
Bayesian multinets over more traditional graphical models is the
ability to represent context-specific independencies--situations
in which subsets of variables exhibit certain conditional independencies
for some, but not all, values of a conditioning variable.
(Further work on context-specific independence has been presented
by Boutilier:96). By making context-specific independencies
explicit as multiple collections of edges, one can obtain (a) more parsimonious
representations of joint probabilities and (b) more efficient inference
algorithms.
In the machine learning setting, however, the advantages of the general
Bayesian multinet formalism are less apparent. Allowing each mixture
component to be a general graphical model forces us to face the difficulties
of learning general graphical structure. Moreover, greedy edge-addition
and edge-deletion algorithms seem particularly ill-suited to the
Bayesian multinet, given that it is the focus on collections of edges
rather than single edges that underlies much of the intuitive appeal
of this architecture.
We view the mixture of trees as providing a reasonable compromise
between the simplicity of tree distributions and the expressive power
of the Bayesian multinet, while doing so within a restricted setting that
leads to efficient machine learning algorithms. In particular, as we show
in this paper, there is a simple generalization of the Chow-Liu algorithm
that makes it possible to find (local) maxima of likelihoods (or penalized
likelihoods) efficiently in general MT models. This algorithm is an
iterative Expectation-Maximization (EM) algorithm, in which the inner
loop (the M step) involves invoking the Chow-Liu algorithm to determine
the structure and parameters of the individual mixture components.
Thus, in a very concrete sense, this algorithm searches in the space
of collections of edges.
In summary, the MT model is a multiple network representation
that shares many of the basic features of Bayesian and Markov network
representations, but brings new features to the fore. We believe that
these features expand the scope of graph-theoretic probabilistic
representations in useful ways and may be particularly appropriate
for machine learning problems.
Subsections


Next: Related work
Up: Learning with Mixtures of
Previous: Learning with Mixtures of
Journal of Machine Learning Research
2000-10-19

