

Next: Learning mixtures of trees
Up: Learning of MT models
Previous: Learning of MT models
Computing the likelihood of a data point under a tree distribution
(in the directed tree representation) takes
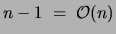 multiplications. Hence, the E step requires
multiplications. Hence, the E step requires 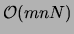 floating
point operations.
As for the M step, the most computationally expensive phase is the
computation of the marginals
floating
point operations.
As for the M step, the most computationally expensive phase is the
computation of the marginals 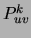 for the
for the 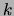 th tree. This step
has time complexity
th tree. This step
has time complexity
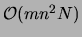 . Another
. Another
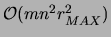 and
and
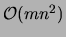 are required at each iteration for the mutual
informations and for the
are required at each iteration for the mutual
informations and for the 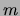 runs of the MWST algorithm.
Finally we need
runs of the MWST algorithm.
Finally we need
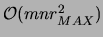 for computing the tree parameters
in the directed representation. The total running time per EM iteration
is thus
for computing the tree parameters
in the directed representation. The total running time per EM iteration
is thus
The algorithm is polynomial (per iteration) in the dimension of
the domain, the number of components and the size of the data set.
The space complexity is also polynomial, and is dominated by
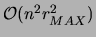 , the space needed to store the pairwise marginal
tables
, the space needed to store the pairwise marginal
tables 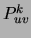 (the tables can be overwritten by successive values of
(the tables can be overwritten by successive values of 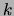 ).
).
Journal of Machine Learning Research
2000-10-19