


Next: Sampling.
Up: Marginalization, inference and sampling
Previous: Marginalization.
Let 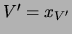 be the
evidence. Then the probability of the hidden variable given evidence
be the
evidence. Then the probability of the hidden variable given evidence
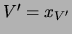 is obtained by applying Bayes' rule as follows:
is obtained by applying Bayes' rule as follows:
In particular, when we observe all but the choice
variable, i.e.,  and
and
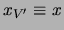 , we obtain the
posterior probability distribution of
, we obtain the
posterior probability distribution of 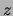 :
:
![\begin{displaymath}
Pr[z=k\vert V=x]\;\equiv\;Pr[z=k\vert x]\;=\;
\frac{\lambda_k T^k(x)}{\sum_{k'}\lambda_{k'}T^{k'}(x)}.
\end{displaymath}](img123.png) |
(4) |
The probability distribution of a given subset of 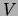 given the evidence is
given the evidence is
Thus the result is again a mixture of the results of inference
procedures run on the component trees.
Journal of Machine Learning Research
2000-10-19
![\begin{displaymath}
Pr[ z=k \vert V'=x_{V'}]\;=\;\frac{ \lambda_k T^k_{V'}(V'=x_{V'})}
{\sum_{k'}\lambda_{k'} T^{k'}_{V'}(V'=x_{V'})}.
\end{displaymath}](img120.png)
![\begin{displaymath}
Pr[ z=k \vert V'=x_{V'}]\;=\;\frac{ \lambda_k T^k_{V'}(V'=x_{V'})}
{\sum_{k'}\lambda_{k'} T^{k'}_{V'}(V'=x_{V'})}.
\end{displaymath}](img120.png)
![\begin{displaymath}
Q_{A\vert V'}(x_A\vert x_{V'})\;=\;
\frac{\sum_{k=1}^m \la...
... Pr[z=k\vert V'=x_{V'}] T^k_{A\vert V'}( x_A \vert x_{V'}).
\end{displaymath}](img124.png)