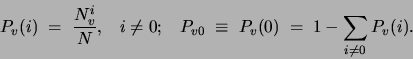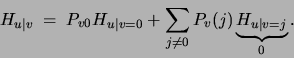

Next: Bibliography
Up: Learning with Mixtures of
Previous: Conclusions
Appendix A.
In this appendix we prove the following theorem from
Section 6.2:
Theorem Let  be discrete variables such that
be discrete variables such that 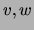 do
not co-occur with
do
not co-occur with 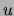 (i.e.,
(i.e.,
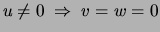 in a given
dataset
in a given
dataset 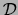 ). Let
). Let 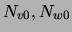 be the number of data points for
which
be the number of data points for
which 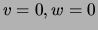 respectively, and let
respectively, and let 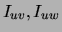 be the
respective empirical mutual information values based on the sample
be the
respective empirical mutual information values based on the sample
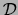 . Then
. Then
with equality only if 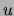 is identically 0.
Proof. We use the notation:
is identically 0.
Proof. We use the notation:
These values represent the (empirical) probabilities of 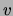 taking value
taking value 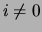 and 0 respectively. Entropies will be denoted
by
and 0 respectively. Entropies will be denoted
by 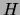 . We aim to show that
. We aim to show that
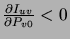 .
We first note a ``chain rule'' expression for the entropy of a discrete
variable. In particular, the entropy
.
We first note a ``chain rule'' expression for the entropy of a discrete
variable. In particular, the entropy 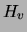 of any multivalued discrete
variable
of any multivalued discrete
variable 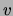 can be decomposed in the following way:
can be decomposed in the following way:
Note moreover that the mutual information of two non-co-occurring variables
is
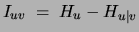 . The second term, the conditional entropy of
. The second term, the conditional entropy of
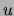 given
given 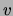 is
is
We now expand 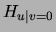 using the decomposition in
(12):
using the decomposition in
(12):
Because 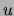 and
and 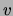 are never non-zero at the same time, all non-zero
values of
are never non-zero at the same time, all non-zero
values of 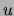 are paired with zero values of
are paired with zero values of 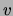 . Consequently
. Consequently
![$Pr[u=i\vert u\not=0,v=0]=Pr[u=i\vert u\neq0]$](img391.png) and
and
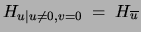 .
The term denoted
.
The term denoted 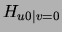 is the entropy of a binary variable whose
probability is
is the entropy of a binary variable whose
probability is ![$Pr[u=0\vert v=0]$](img394.png) . This probability equals
. This probability equals
Note that in order to obtain a non-negative probability in the above
equation one needs
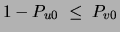 , a condition that is
always satisfied if
, a condition that is
always satisfied if 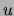 and
and 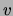 do not co-occur. Replacing the previous
three equations in the formula of the mutual information, we get
do not co-occur. Replacing the previous
three equations in the formula of the mutual information, we get
This expression, remarkably, depends only on 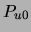 and
and 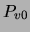 .
Taking its partial derivative with respect to
.
Taking its partial derivative with respect to
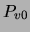 yields
yields
a value that is always negative, independently of 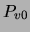 . This shows
the mutual information increases monotonically with the ``occurrence frequency'' of
. This shows
the mutual information increases monotonically with the ``occurrence frequency'' of
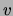 given by
given by 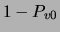 . Note also that the above expression for the
derivative is the same as the result obtained for binary variables
in (11).
. Note also that the above expression for the
derivative is the same as the result obtained for binary variables
in (11).


Next: Bibliography
Up: Learning with Mixtures of
Previous: Conclusions
Journal of Machine Learning Research
2000-10-19