


Next: Appendix A.
Up: Learning with Mixtures of
Previous: Experiments
Conclusions
We have presented the mixture of trees (MT), a probabilistic
model in which joint probability distributions are represented as
finite mixtures of tree distributions. Tree distributions have a number
of virtues--representational, computational and statistical--but have
limited expressive power. Bayesian and Markov networks achieve
significantly greater expressive power while retaining many of
the representational virtues of trees, but incur significantly higher
costs on the computational and statistical fronts. The mixture approach
provides an alternative upgrade path. While Bayesian and Markov
networks have no distinguished relationships between edges, and statistical
model selection procedures for these networks generally involve
additions and deletions of single edges, the MT model groups
overlapping sets of edges into mixture components, and edges are
added and removed via a maximum likelihood algorithm that is
constrained to fit tree models in each mixture component. We have
also seen that it is straightforward to develop Bayesian methods that
allow finer control over the choice of edges and smooth the numerical
parameterization of each of the component models.
[Chow, Liu 1968] presented the basic maximum
likelihood algorithm for fitting tree distributions that provides
the M step of our EM algorithm, and also showed how to use ensembles
of trees to solve classification problems, where each tree
models the class-conditional density of one of the classes.
This approach was pursued by
[Friedman, Geiger, Goldszmidt
1997,[Friedman, Goldszmidt, Lee
1998], who
emphasized the connection with the naive Bayes model, and
presented empirical results that demonstrated the performance gains
that could be obtained by enhancing naive Bayes to allow connectivity
between the attributes. Our work is a further contribution to
this general line of research--we treat an ensemble of trees as
a mixture distribution. The mixture approach provides additional
flexibility in the classification domain, where the ``choice variable''
need not be the class label, and also allows the architecture to be
applied to unsupervised learning problems.
The algorithms for learning and inference that we have presented
have relatively benign scaling: inference is linear in the
dimensionality 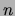 and each step of the EM learning algorithm is quadratic
in
and each step of the EM learning algorithm is quadratic
in 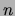 . Such favorable time complexity is an important virtue of our
tree-based approach. In particularly large problems, however,
such as those that arise in information retrieval applications,
quadratic complexity can become onerous. To allow the use of
the MT model to such cases, we have developed the ACCL algorithm,
where by exploiting data sparseness and paying attention to data
structure issues we have significantly reduced run time: We presented
examples in which the speed-up obtained from the ACCL algorithm
was three orders of magnitude.
Are there other classes of graphical models whose structure can
be learned efficiently from data? Consider the class of Bayesian
networks for which the topological ordering of the variables is
fixed and the number of parents of each node is bounded by a fixed
constant
. Such favorable time complexity is an important virtue of our
tree-based approach. In particularly large problems, however,
such as those that arise in information retrieval applications,
quadratic complexity can become onerous. To allow the use of
the MT model to such cases, we have developed the ACCL algorithm,
where by exploiting data sparseness and paying attention to data
structure issues we have significantly reduced run time: We presented
examples in which the speed-up obtained from the ACCL algorithm
was three orders of magnitude.
Are there other classes of graphical models whose structure can
be learned efficiently from data? Consider the class of Bayesian
networks for which the topological ordering of the variables is
fixed and the number of parents of each node is bounded by a fixed
constant 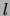 . For this class the optimal model structure for a
given target distribution can be found in
. For this class the optimal model structure for a
given target distribution can be found in
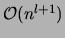 time
by a greedy algorithm. These models share with trees the property
of being matroids [West 1996]. The matroid is the unique
algebraic structure for which the ``maximum weight'' problem, in
particular the maximum weight spanning tree problem, is solved optimally
by a greedy algorithm. Graphical models that are matroids have
efficient structure learning algorithms; it is an interesting
open problem to find additional examples of such models.
We would like to acknowledge support for this project
from the National Science Foundation (NSF grant IIS-9988642)
and the Multidisciplinary Research Program of the Department
of Defense (MURI N00014-00-1-0637).
time
by a greedy algorithm. These models share with trees the property
of being matroids [West 1996]. The matroid is the unique
algebraic structure for which the ``maximum weight'' problem, in
particular the maximum weight spanning tree problem, is solved optimally
by a greedy algorithm. Graphical models that are matroids have
efficient structure learning algorithms; it is an interesting
open problem to find additional examples of such models.
We would like to acknowledge support for this project
from the National Science Foundation (NSF grant IIS-9988642)
and the Multidisciplinary Research Program of the Department
of Defense (MURI N00014-00-1-0637).



Next: Appendix A.
Up: Learning with Mixtures of
Previous: Experiments
Journal of Machine Learning Research
2000-10-19