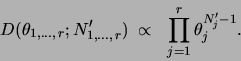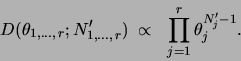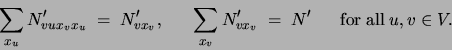Next: Experiments
Up: Decomposable priors and MAP
Previous: Decomposable priors for tree
The decomposable prior for parameters that we introduce is a
Dirichlet prior [Heckerman, Geiger, Chickering
1995]. The Dirichlet distribution
is defined over the domain of
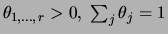 and has the form
and has the form
The numbers
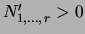 that parametrize
that parametrize 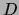 can be interpreted as the sufficient statistics of a ``fictitious
data set'' of size
can be interpreted as the sufficient statistics of a ``fictitious
data set'' of size
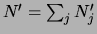 . Therefore
. Therefore 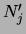 are called
fictitious counts.
are called
fictitious counts. 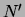 represents the strength of the prior.
To specify a prior for tree parameters, one must
specify a Dirichlet distribution for each of the
probability tables
represents the strength of the prior.
To specify a prior for tree parameters, one must
specify a Dirichlet distribution for each of the
probability tables
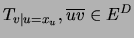 , for each possible tree structure
, for each possible tree structure 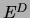 . This is achieved by
means of a set of parameters
. This is achieved by
means of a set of parameters 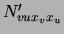 satisfying
satisfying
With these settings, the prior for the parameters
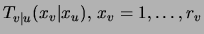 in any tree that contains the directed edge
in any tree that contains the directed edge
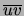 is defined by
is defined by
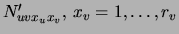 . This
representation of the prior is not only compact (order
. This
representation of the prior is not only compact (order 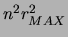 parameters) but it is
also consistent: two different directed parametrizations of the same
tree distribution receive the same prior. The assumptions allowing us to
define this prior are explicated by MJa:uai00 and
parallel the reasoning of heckerman:95 for general Bayes nets.
Denote by
parameters) but it is
also consistent: two different directed parametrizations of the same
tree distribution receive the same prior. The assumptions allowing us to
define this prior are explicated by MJa:uai00 and
parallel the reasoning of heckerman:95 for general Bayes nets.
Denote by 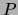 the empirical distribution obtained from a data set of
size
the empirical distribution obtained from a data set of
size 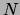 and by
and by
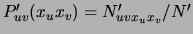 the
distribution defined by the fictitious counts. Then, by a property of the Dirichlet distribution [Heckerman, Geiger, Chickering
1995] it follows that learning a MAP tree
is equivalent to learning an ML tree for the weighted
combination
the
distribution defined by the fictitious counts. Then, by a property of the Dirichlet distribution [Heckerman, Geiger, Chickering
1995] it follows that learning a MAP tree
is equivalent to learning an ML tree for the weighted
combination 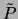 of the two ``datasets''
of the two ``datasets''
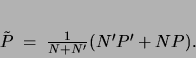 |
(10) |
Consequently, the parameters of the optimal tree will be
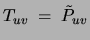 .
For a mixture of trees, maximizing the posterior translates into
replacing
.
For a mixture of trees, maximizing the posterior translates into
replacing 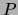 by
by 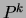 and
and 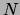 by
by 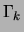 in equation
(10) above. This implies that the M
step of the EM algorithm, as well as the E step, is exact and
tractable in the case of MAP estimation with decomposable
priors.
Finally, note that the posteriors
in equation
(10) above. This implies that the M
step of the EM algorithm, as well as the E step, is exact and
tractable in the case of MAP estimation with decomposable
priors.
Finally, note that the posteriors
![$Pr[ Q\vert{\cal D}]$](img172.png) for models
with different
for models
with different 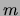 are defined up to a constant that depends on
are defined up to a constant that depends on
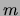 . Hence, one cannot compare posteriors of MTs with different
numbers of mixture components
. Hence, one cannot compare posteriors of MTs with different
numbers of mixture components 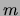 . In the experiments that
we present, we chose
. In the experiments that
we present, we chose 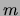 via other performance criteria:
validation set likelihood in the density estimation experiments
and validation set classification accuracy in the classification
tasks.
via other performance criteria:
validation set likelihood in the density estimation experiments
and validation set classification accuracy in the classification
tasks.



Next: Experiments
Up: Decomposable priors and MAP
Previous: Decomposable priors for tree
Journal of Machine Learning Research
2000-10-19