Decomposable priors and MAP estimation for mixtures of trees

The Bayesian learning framework combines information obtained from direct observations with prior knowledge about the model, when the latter is represented as a probability distribution. The object of interest of Bayesian analysis is the posterior distribution over the models given the observed data, $Pr[ Q\vert{\cal D}]$, a quantity which can rarely be calculated explicitly. 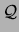Practical methods for approximating the posterior include choosing a single maximum a posteriori (MAP) estimate, replacing the continuous space of models by a finite set ${\cal Q}$ of high posterior probability [Heckerman, Geiger, Chickering 1995], and expanding the posterior around its mode(s) [Cheeseman, Stutz 1995]. Finding the local maxima (modes) of the distribution $Pr[ Q\vert{\cal D}]$ is a necessary step in all the above methods and is our primary concern in this section. We demonstrate that maximum a posteriori modes can be found as efficiently as maximum likelihood modes, given a particular choice of prior. This has two consequences: First, it makes approximate Bayesian averaging possible. Second, if one uses a non-informative prior, then MAP estimation is equivalent to Bayesian smoothing, and represents a form of regularization. Regularization is particularly useful in the case of small data sets in order to prevent overfitting.