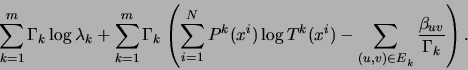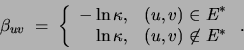Next: Decomposable priors for tree
Up: Decomposable priors and MAP
Previous: MAP estimation by the
The general form of a decomposable prior for the tree structure  is
one where each edge contributes a constant factor independent of the
presence or absence of other edges in
is
one where each edge contributes a constant factor independent of the
presence or absence of other edges in  :
:
With this prior, the expression to be maximized in the M step of the
EM algorithm becomes
Consequently, each edge weight 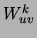 in tree
in tree 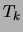 is adjusted by
the corresponding value
is adjusted by
the corresponding value 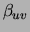 divided by the total number
of points that tree
divided by the total number
of points that tree 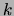 is responsible for:
is responsible for:
A negative 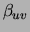 increases the probability of
increases the probability of 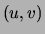 being
present in the final solution, whereas a positive value of
being
present in the final solution, whereas a positive value of 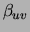 acts like a penalty on the presence of edge
acts like a penalty on the presence of edge 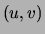 in the tree.
If the MWST procedure is modified so as
to not add negative-weight edges, one can obtain
(disconnected) trees having fewer than
in the tree.
If the MWST procedure is modified so as
to not add negative-weight edges, one can obtain
(disconnected) trees having fewer than 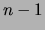 edges. Note that the
strength of the prior is inversely proportional to
edges. Note that the
strength of the prior is inversely proportional to 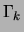 , the
total number of data points assigned to mixture component
, the
total number of data points assigned to mixture component 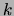 . Thus,
with equal priors for all trees
. Thus,
with equal priors for all trees 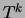 , trees accounting for fewer data
points will be penalized more strongly and therefore will be likely to
have fewer edges.
If one chooses the edge penalties to be proportional to the increase
in the number of parameters caused by the addition of edge
, trees accounting for fewer data
points will be penalized more strongly and therefore will be likely to
have fewer edges.
If one chooses the edge penalties to be proportional to the increase
in the number of parameters caused by the addition of edge 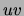 to the
tree,
to the
tree,
then a Minimum Description Length (MDL) [Rissanen 1989] type of
prior is implemented.
In the context of learning Bayesian networks,
heckerman:95 suggested the following prior:
where 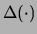 is a distance metric between Bayes net
structures and
is a distance metric between Bayes net
structures and 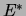 is the prior network structure. Thus, this
prior penalizes deviations from the prior network.
This prior is decomposable, entailing
is the prior network structure. Thus, this
prior penalizes deviations from the prior network.
This prior is decomposable, entailing
Decomposable priors on structure can also be used when the structure
is common for all trees (MTSS). In this case the effect of the prior
is to penalize the weight 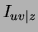 in (8) by
in (8) by
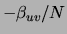 .
A decomposable prior has the remarkable property that its
normalization constant can be computed exactly in closed form. This
makes it possible not only to completely define the prior, but also to
compute averages under this prior (e.g., to compute a model's
evidence). Given that the number of all undirected tree structures
over
.
A decomposable prior has the remarkable property that its
normalization constant can be computed exactly in closed form. This
makes it possible not only to completely define the prior, but also to
compute averages under this prior (e.g., to compute a model's
evidence). Given that the number of all undirected tree structures
over 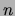 variables is
variables is 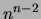 , this result [Meila, Jaakkola 2000]
is quite surprising.
, this result [Meila, Jaakkola 2000]
is quite surprising.



Next: Decomposable priors for tree
Up: Decomposable priors and MAP
Previous: MAP estimation by the
Journal of Machine Learning Research
2000-10-19
![\begin{displaymath}
Pr[E] \;\propto\; \prod_{{(u,v) \in E}} \exp(-\beta_{uv}).
\end{displaymath}](img181.png)
![\begin{displaymath}
Pr[E] \;\propto\; \prod_{{(u,v) \in E}} \exp(-\beta_{uv}).
\end{displaymath}](img181.png)