Definition and Basic Properties

Given a domain of interest having a set of finite variables ${\bf X}=(X_1,\ldots,X_n)$, let ${\cal P} = (p_1(x_1\vert{\bf x}\setminus x_1), p_2(x_2\vert{\bf x}\setminus x_2), \ldots, p_n(x_n\vert{\bf x}\setminus x_m))$ be a set of conditional distributions, one for each variable in ${\bf X}$. In normal use, these distributions are intended to correspond to classifications/regressions learned from a single data set but, formally, they can be any set of conditional distributions. We do not require that these distributions be consistent--that is, we do not require that they can be obtained via inference from a single joint distribution $p({\bf x})$. A dependency network for ${\bf X}$ and ${\cal P}$ is a pair $({\cal G},{\cal P}')$ where ${\cal G}$ is a (usually cyclic) directed graph and ${\cal P}'$ is a set of conditional probability distributions satisfying

$$p_i(x_i\vert{\bf pa}_i) = p_i(x_i\vert{\bf x}\setminus x_i)$$

for every $p_i$ in ${\cal P}$. Again, we call the set of conditional distributions $p_i(x_i\vert{\bf pa}_i), i=1,\ldots,n$ the local probability distributions for the dependency network. In most graphical modeling research, a graphical model is used to define a joint distribution for its variables. We do the same using a dependency network. In particular, the procedure of the ordered Gibbs sampler described in the previous section, when applied to a dependency network, yields a joint distribution for the domain. The result holds whether or not the local distributions in the dependency network are consistent. More formally, we have the following theorem, which is established by tracing the proof of Theorem 2 given in the previous section and noting that it does not rely on the consistency of the distributions.

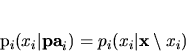
Theorem 3: The procedure of an ordered Gibbs sampler applied to a dependency network for ${\bf X}$ and ${\cal P}$, where each $X_i$ is finite (and hence discrete) and each local distribution in ${\cal P}$ is positive, defines a Markov chain with a unique stationary joint distribution for ${\bf X}$ that can be reached from any initial state of the chain.

Technically speaking, the procedure of Gibbs sampling applied to an inconsistent dependency network is not itself a Gibbs sampler, because there is no joint distribution consistent with all the local distributions. Consequently, we call this procedure an ordered pseudo-Gibbs sampler. One rather disturbing property of this procedure is that it produces a joint distribution that is likely to be inconsistent with many of the conditional distributions used to produce it. Nonetheless, as we have suggested and shall examine further, when each of the local distributions of a dependency network are learned from the same data, these distributions should be almost consistent with the joint distribution. Another disturbing observation is that the joint distribution obtained will depend on the order in which the pseudo-Gibbs sampler visits the variables. For example, consider the dependency network with the structure $X_1 \rightarrow X_2$, saying that $X_2$ depends on $X_1$ but $X_1$ does not depend on $X_2$. If we draw sample-pairs $(x_1,x_2)$--that is, $x_1$ and then $x_2$--then the resulting stationary distribution will have $X_1$ and $X_2$ dependent. In contrast, if we draw sample-pairs $(x_2,x_1)$, then the resulting stationary distribution will have $X_1$ and $X_2$ independent. Due to the near consistency of the local distributions, however, the joint distributions obtained from different orderings will be close. If we indeed discover the dependency-network structure $X_1 \rightarrow X_2$ in practice, then $X_1$ and $X_2$ must be ``almost'' independent. Given a graphical model for a domain and an ordered Gibbs sampler that extracts a joint distribution from that model, we can apply the rules of probability to this joint distribution to answer probabilistic queries. Alternatively, we can apply Algorithm 1 directly to a given dependency network. Such an application may yield different answers than those computed from the joint distribution obtained from the dependency network, but can be justified heuristically due to near consistency. In Sections 3.3 and 3.4, we examine the issue of near consistency more carefully. In the remainder of this section, we mention two basic properties of dependency networks. First, let us consider the distributions that can be represented by a general dependency-network structure. Unlike the situation for consistent dependency networks, a general dependency-network structure and a Markov network structure with the same adjacencies do not represent the same distributions. In fact, a dependency network with a given structure defines a larger set of distributions than a Markov network with the same adjacencies. As an example, consider the dependency-network structure $X_1 \leftrightarrow X_2 \leftrightarrow X_3$. In a simple experiment, we sampled local distributions for this structure from a uniform distribution. We then computed the stationary distribution of the Markov chain defined by a pseudo-Gibbs sampler with variable order $(X_1,X_3,X_2)$. In all runs, we found that $X_1$ and $X_3$ were conditionally dependent given $X_2$ in the stationary distribution. In a Markov network with the same adjacencies, $X_1$ and $X_3$ must be conditionally independent given $X_2$. Second, let us consider a simple necessary condition for consistency. We say that a dependency network for ${\bf X}$ is bi-directional if $X_i$ is a parent of $X_j$ if and only if $X_j$ is a parent of $X_i$, for all $X_i$ and $X_j$ in ${\bf X}$. In addition, let ${\bf pa}_i^j$ be the $j^{th}$ parent of node $X_i$. We say that a consistent dependency network is minimal if and only if, for every node $X_i$ and for every parent ${\bf pa}_i^j$, $X_i$ is not independent of ${\bf pa}_i^j$ given the remaining parents of $X_i$. With these definitions, we have the following theorem, proved in the Appendix.

Theorem 4: A minimal consistent dependency network for a positive distribution $p({\bf x})$ must be bi-directional.