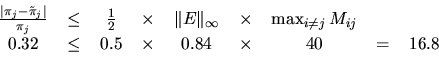

Next: Related Work
Up: General Dependency Networks
Previous: Probabilistic Inference With Real
Near Consistency: Theoretical Considerations
Our concerns of the previous section were motivated by the possibility
that small deviations in the local distributions of a dependency
network could be amplified by the process of pseudo-Gibbs sampling.
In this section, we examine this concern more directly and from a
theoretical perspective.
Consider two dependency networks: one learned from data and another
that encodes the true distribution from which the data was sampled.
Note that it is always possible to find a dependency network that
encodes the true distribution--for example, a fully-connected
dependency network can encode any joint distribution. Let 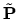 and
and
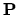 denote the transition matrices of the Markov chains defined by
the learned and truth-encoding dependency networks, respectively. In
addition, let
denote the transition matrices of the Markov chains defined by
the learned and truth-encoding dependency networks, respectively. In
addition, let
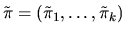 and
and
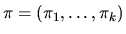 denote the stationary distributions
corresponding to
denote the stationary distributions
corresponding to 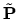 and
and 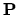 , respectively. Our concern about
sensitivity to deviations in local distributions can now be phrased as
follows: If
, respectively. Our concern about
sensitivity to deviations in local distributions can now be phrased as
follows: If 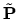 is close to
is close to 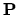 , will
, will
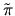 be close
be close 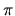 ?
There is a large literature in an area generally known as perturbation
theory of stochastic matrices that provides answers to this question
for various notions of ``close''. Answers usually are of the form
?
There is a large literature in an area generally known as perturbation
theory of stochastic matrices that provides answers to this question
for various notions of ``close''. Answers usually are of the form
where
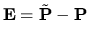 ,
, 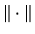 is some norm, and
is some norm, and 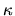 or
or
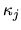 are measures of sensitivity called condition numbers.
When working with probabilities, where relative as opposed to absolute
errors are often important, bounds of the form shown in
Equation 6 are particularly useful. Here, we cite a
potentially useful bound of this form given by Cho and Meyer
(1999). These authors provide references to many other
bounds as well.
are measures of sensitivity called condition numbers.
When working with probabilities, where relative as opposed to absolute
errors are often important, bounds of the form shown in
Equation 6 are particularly useful. Here, we cite a
potentially useful bound of this form given by Cho and Meyer
(1999). These authors provide references to many other
bounds as well.
Theorem (Cho and Meyer, 1999): Let 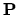 and
and
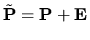 be transition matrices for two homogenous, irreducible
be transition matrices for two homogenous, irreducible
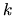 -state Markov chains with respective stationary distributions
-state Markov chains with respective stationary distributions
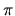 and
and
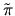 . Let
. Let
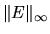 denote the infinity-norm
of E, the maximum over
denote the infinity-norm
of E, the maximum over 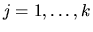 of the column sums
of the column sums
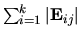 . Let
. Let 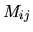 denote the mean first passage
time from the
denote the mean first passage
time from the 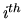 state to the
state to the 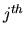 state in the chain
corresponding to
state in the chain
corresponding to 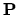 --that is, the expected number of transitions
to move from state
--that is, the expected number of transitions
to move from state 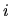 to state
to state 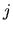 . Then, the relative change in the
. Then, the relative change in the
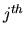 stationary probability
stationary probability 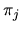 is given by
is given by
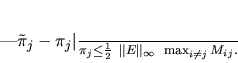 |
(7) |
Their bound is tight in the sense that, for any 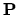 satisfying the conditions of the theorem, there exists a perturbation
satisfying the conditions of the theorem, there exists a perturbation
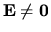 such that the inequality in Equation 7
can be replaced with an equality. Nonetheless, when applied to
dependency networks, the bound is typically not tight. To illustrate
this point, we computed each term in Equation 7 for a
transition matrix
such that the inequality in Equation 7
can be replaced with an equality. Nonetheless, when applied to
dependency networks, the bound is typically not tight. To illustrate
this point, we computed each term in Equation 7 for a
transition matrix 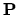 corresponding to the Bayesian network learned
from 790 cases from the WAM data set, and a
corresponding to the Bayesian network learned
from 790 cases from the WAM data set, and a 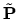 corresponding to a
dependency network learned from a random sample of 790 cases generated
from that Bayesian network. For
corresponding to a
dependency network learned from a random sample of 790 cases generated
from that Bayesian network. For 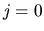 , the state corresponding to
, the state corresponding to
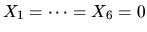 in the WAM domain, we obtain the inequality
in the WAM domain, we obtain the inequality
which is far from tight.
Nonetheless, the appearance of mixing time in Equation 7
is interesting. It suggests that that chains with good convergence
properties will be insensitive to perturbations in the transition
matrix. In particular, it suggests that the joint distribution
defined by a dependency network is more likely to be insensitive to
errors in the local distributions of the network precisely when Gibbs
sampling is effective. Hopefully, additional research will produce
tighter bounds that better characterize those situations in which
dependency networks can be used safely.


Next: Related Work
Up: General Dependency Networks
Previous: Probabilistic Inference With Real
Journal of Machine Learning Research,
2000-10-19
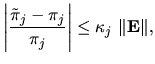
![]() and
and
![]() be transition matrices for two homogenous, irreducible
be transition matrices for two homogenous, irreducible
![]() -state Markov chains with respective stationary distributions
-state Markov chains with respective stationary distributions
![]() and
and
![]() . Let
. Let
![]() denote the infinity-norm
of E, the maximum over
denote the infinity-norm
of E, the maximum over ![]() of the column sums
of the column sums
![]() . Let
. Let ![]() denote the mean first passage
time from the
denote the mean first passage
time from the ![]() state to the
state to the ![]() state in the chain
corresponding to
state in the chain
corresponding to ![]() --that is, the expected number of transitions
to move from state
--that is, the expected number of transitions
to move from state ![]() to state
to state ![]() . Then, the relative change in the
. Then, the relative change in the
![]() stationary probability
stationary probability ![]() is given by
is given by
![]() satisfying the conditions of the theorem, there exists a perturbation
satisfying the conditions of the theorem, there exists a perturbation
![]() such that the inequality in Equation 7
can be replaced with an equality. Nonetheless, when applied to
dependency networks, the bound is typically not tight. To illustrate
this point, we computed each term in Equation 7 for a
transition matrix
such that the inequality in Equation 7
can be replaced with an equality. Nonetheless, when applied to
dependency networks, the bound is typically not tight. To illustrate
this point, we computed each term in Equation 7 for a
transition matrix ![]() corresponding to the Bayesian network learned
from 790 cases from the WAM data set, and a
corresponding to the Bayesian network learned
from 790 cases from the WAM data set, and a ![]() corresponding to a
dependency network learned from a random sample of 790 cases generated
from that Bayesian network. For
corresponding to a
dependency network learned from a random sample of 790 cases generated
from that Bayesian network. For ![]() , the state corresponding to
, the state corresponding to
![]() in the WAM domain, we obtain the inequality
in the WAM domain, we obtain the inequality