

Next: Definition and Basic Properties
Up: Dependency Networks for Inference,
Previous: Probabilistic Inference
General Dependency Networks
As we have discussed, consistent dependency networks and Markov
networks are interchangeable representations: given one, we can
compute the other. In this section, we consider a more general class
of dependency networks and part company with Markov networks.
Our extension of consistent dependency networks is motivated by
computational concerns. For domains having a large number of
variables and many dependencies among those variables, it is
computationally expensive to learn a Markov network from data and then
convert that network to a consistent dependency network. As an
alternative, we start with the observation that the local distribution
for variable 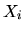 in a dependency network is the conditional
distribution
in a dependency network is the conditional
distribution
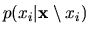 , which can be estimated by any
number of probabilistic classification techniques (or regression
techniques, if we were to consider continuous variables) such as
methods using a probabilistic decision tree (e.g., Buntine,
1991), a generalized linear model (e.g., McCullagh
and Nelder, 1989), a neural network (e.g., Bishop,
1995), a probabilistic support-vector machine (e.g.,
Platt, 1999), or an embedded regression/classification
model (Heckerman and Meek, 1997). This observation
suggests a simple, heuristic approach for learning the structure and
probabilities of a dependency network from exchangeable (i.i.d.) data.
Namely, for each variable
, which can be estimated by any
number of probabilistic classification techniques (or regression
techniques, if we were to consider continuous variables) such as
methods using a probabilistic decision tree (e.g., Buntine,
1991), a generalized linear model (e.g., McCullagh
and Nelder, 1989), a neural network (e.g., Bishop,
1995), a probabilistic support-vector machine (e.g.,
Platt, 1999), or an embedded regression/classification
model (Heckerman and Meek, 1997). This observation
suggests a simple, heuristic approach for learning the structure and
probabilities of a dependency network from exchangeable (i.i.d.) data.
Namely, for each variable 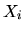 in domain
in domain 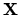 , we
independently estimate its local distribution from data using a
classification algorithm. Once we have all estimates for the local
distributions, we then construct the structure of the dependency
network from the (in)dependencies encoded in these estimates.
For example, suppose we wish to construct a
dependency network for the domain
, we
independently estimate its local distribution from data using a
classification algorithm. Once we have all estimates for the local
distributions, we then construct the structure of the dependency
network from the (in)dependencies encoded in these estimates.
For example, suppose we wish to construct a
dependency network for the domain
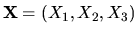 . To do so, we
need to estimate three conditional probability distributions:
. To do so, we
need to estimate three conditional probability distributions:
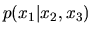 ,
,
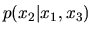 , and
, and
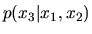 . First, we
use prior knowledge to decide how each distribution is to be modeled.
We may decide, for example, that a logistic regression, a multilayer
neural net, and a probabilistic decision tree are appropriate models
for
. First, we
use prior knowledge to decide how each distribution is to be modeled.
We may decide, for example, that a logistic regression, a multilayer
neural net, and a probabilistic decision tree are appropriate models
for
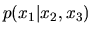 ,
,
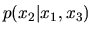 , and
, and
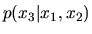 ,
respectively. (There is no requirement that each distribution be
chosen from the same model class.) In addition, for each estimation,
we may choose to use a feature-selection algorithm that can discard
some of the inputs. Next, we apply the estimation/learning
procedures. For the sake of illustration, suppose we discover that
,
respectively. (There is no requirement that each distribution be
chosen from the same model class.) In addition, for each estimation,
we may choose to use a feature-selection algorithm that can discard
some of the inputs. Next, we apply the estimation/learning
procedures. For the sake of illustration, suppose we discover that
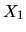 is not a significant predictor of
is not a significant predictor of 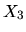 and that
and that 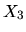 is not a
significant predictor of
is not a
significant predictor of 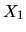 . Finally, we construct the dependency
network structure--in this case,
. Finally, we construct the dependency
network structure--in this case,
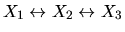 --and populate the local distributions with the
conditional-probability estimates. Note that feature selection in the
classification/regression process governs the structure of the
dependency network.
This algorithm will be computationally efficient in many situations
where learning a Markov network and converting it to a dependency
network is not. Nonetheless, this procedure has the drawback that,
due to--for example--heuristic search and finite-data effects, the
resulting local distributions are likely to be inconsistent in
that there is no joint distribution
--and populate the local distributions with the
conditional-probability estimates. Note that feature selection in the
classification/regression process governs the structure of the
dependency network.
This algorithm will be computationally efficient in many situations
where learning a Markov network and converting it to a dependency
network is not. Nonetheless, this procedure has the drawback that,
due to--for example--heuristic search and finite-data effects, the
resulting local distributions are likely to be inconsistent in
that there is no joint distribution 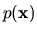 from which each of the
local distributions may be obtained via the rules of probability. For
example, in the simple domain
from which each of the
local distributions may be obtained via the rules of probability. For
example, in the simple domain
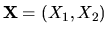 it is possible that the
estimator of
it is possible that the
estimator of 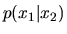 discards
discards 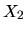 as an input whereas the
estimator of
as an input whereas the
estimator of 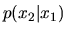 retains
retains 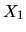 as an input. The result is
the structural inconsistency that
as an input. The result is
the structural inconsistency that 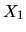 helps to predict
helps to predict 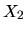 , but
, but
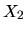 does not help to predict
does not help to predict 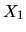 . Numeric inconsistencies are
also likely to result. Nonetheless, in situations where the data set
contains many samples, strong inconsistencies will be rare because
each local distribution is learned from the same data set, which we
assume is generated from a single underlying joint distribution. In
other words, although dependency networks learned using our procedure
will be inconsistent, they will be ``almost'' consistent when learned
from data sets with large sample sizes. This observation assumes that
the model classes used for the local distributions can closely
approximate the conditional distributions consistent with the
underlying joint distribution. For example, probabilistic decision
trees, which we shall use, satisfy this assumption for variables with
finite domains.
Because a dependency network learned in this manner is almost
consistent, we can imagine--as a heuristic--using procedures
resembling Gibbs sampling to extract a joint distribution and to
answer probabilistic queries. In the remainder of this section, we
formalize these ideas and evaluate them with experiments on real data.
. Numeric inconsistencies are
also likely to result. Nonetheless, in situations where the data set
contains many samples, strong inconsistencies will be rare because
each local distribution is learned from the same data set, which we
assume is generated from a single underlying joint distribution. In
other words, although dependency networks learned using our procedure
will be inconsistent, they will be ``almost'' consistent when learned
from data sets with large sample sizes. This observation assumes that
the model classes used for the local distributions can closely
approximate the conditional distributions consistent with the
underlying joint distribution. For example, probabilistic decision
trees, which we shall use, satisfy this assumption for variables with
finite domains.
Because a dependency network learned in this manner is almost
consistent, we can imagine--as a heuristic--using procedures
resembling Gibbs sampling to extract a joint distribution and to
answer probabilistic queries. In the remainder of this section, we
formalize these ideas and evaluate them with experiments on real data.
Subsections


Next: Definition and Basic Properties
Up: Dependency Networks for Inference,
Previous: Probabilistic Inference
Journal of Machine Learning Research,
2000-10-19