

Next: Probabilistic Inference With Real
Up: General Dependency Networks
Previous: Definition and Basic Properties
When learning a dependency network from data, a variety of
classification/regression techniques may be used to estimate the local
distributions. We have used methods based on probabilistic decision
trees (e.g., Buntine, 1991) and probabilistic
support vector machines (e.g., Platt, 1999). For
simplicity, we limit our discussion in this paper to the use of
probabilistic decision trees.
In this approach, for each variable 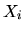 in
in 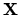 , we learn a
probabilistic decision tree where
, we learn a
probabilistic decision tree where 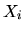 is the target variable and
is the target variable and
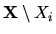 are the input variables. Each leaf is modeled as
a multinomial distribution. To learn the decision-tree structure, we
use a simple hill-climbing approach in conjunction with a Bayesian
score (posterior probability of model structure) as described by
Friedman and Goldszmdit (1996) and Chickering,
Heckerman, and Meek (1997). To learn a decision-tree
structure for
are the input variables. Each leaf is modeled as
a multinomial distribution. To learn the decision-tree structure, we
use a simple hill-climbing approach in conjunction with a Bayesian
score (posterior probability of model structure) as described by
Friedman and Goldszmdit (1996) and Chickering,
Heckerman, and Meek (1997). To learn a decision-tree
structure for 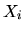 , we initialize the search algorithm with a
singleton root node having no children. Then, we replace each leaf
node in the tree with a binary split on some variable
, we initialize the search algorithm with a
singleton root node having no children. Then, we replace each leaf
node in the tree with a binary split on some variable 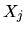 in
in
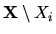 , until no such replacement increases the score of the
tree. Our binary split on
, until no such replacement increases the score of the
tree. Our binary split on 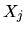 is a decision-tree node with
two children: one of the children corresponds to a particular value of
is a decision-tree node with
two children: one of the children corresponds to a particular value of
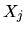 , and the other child corresponds to all other values of
, and the other child corresponds to all other values of
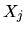 . Our Bayesian scoring function uses a uniform prior distribution
for the parameters of all multinomial distributions, and a structure
prior proportional to
. Our Bayesian scoring function uses a uniform prior distribution
for the parameters of all multinomial distributions, and a structure
prior proportional to 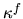 , where
, where 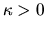 is a tunable
parameter and
is a tunable
parameter and 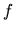 is the number of free parameters in the decision
tree. In studies that predated those described in this paper, we have
found that the setting
is the number of free parameters in the decision
tree. In studies that predated those described in this paper, we have
found that the setting 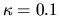 yields accurate predictions over
a wide variety of datasets. We use this same setting in the
experiments described in this paper.
yields accurate predictions over
a wide variety of datasets. We use this same setting in the
experiments described in this paper.


Next: Probabilistic Inference With Real
Up: General Dependency Networks
Previous: Definition and Basic Properties
Journal of Machine Learning Research,
2000-10-19