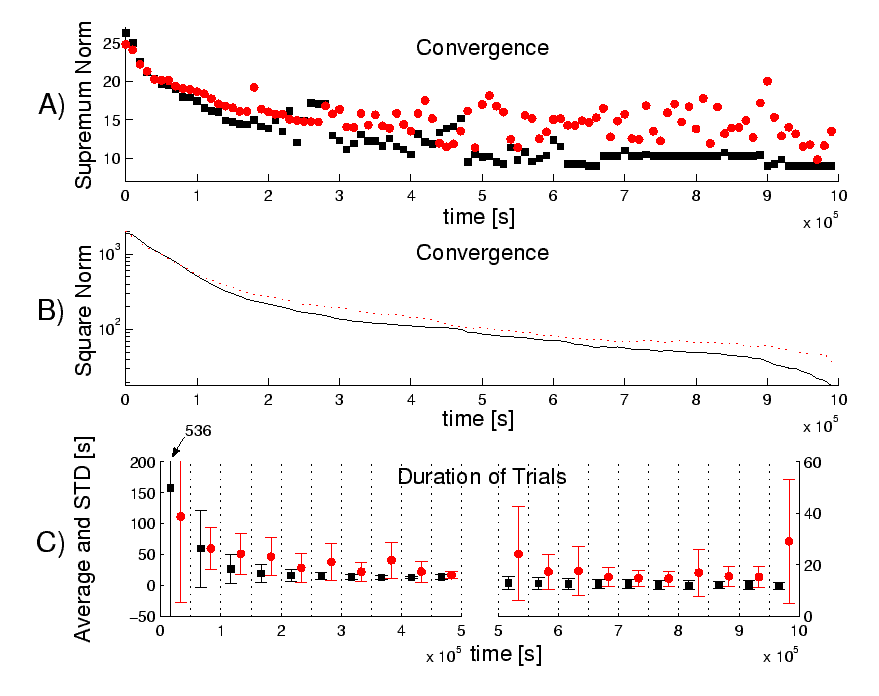
Convergence properties of the event-value function for the two-link pendulum are shown in Figure 5. The experiment concerns crude discretization of the state space. No change of the parameters of the pendulum are made. However, crude discretization of the environment and a robust controller, which is part of the environment, exhibits itself as a varying environment.
The theorems of Section 3 concern supremum norm. Two
curves about the supremum norm are shown in
Figure 5A, one with the SDS controller turned
off (![]() ) and another one with the SDS controller on
) and another one with the SDS controller on
![]() . Convergence occurs for learning with the
SDS controller `on'.10 Interestingly, convergence is faster with the
SDS controller than without it. This is a consequence of the
larger variety of actions available when the robust controller is
applied.
. Convergence occurs for learning with the
SDS controller `on'.10 Interestingly, convergence is faster with the
SDS controller than without it. This is a consequence of the
larger variety of actions available when the robust controller is
applied.
The square norm against the last event-value function of this
series of experiments (Figure 5B) may provide
insight into the performance of the two-link pendulum. The
performance of the pendulum can be characterized by the average
task duration and the standard deviation of task duration during
the course of learning (Figure 5C). There is a
clear advantage for the
![]() case against learning
without the robust controller.
case against learning
without the robust controller.
|