


Next: 4. LSVM for Nonlinear
Up: Lagrangian Support Vector Machines
Previous: 2. The Linear Support
3. LSVM (Lagrangian Support Vector Machine) Algorithm
Before stating our algorithm we define two matrices to simplify
notation as follows:
![\begin{displaymath}
H=D[A\;\;\;-e],\;\;\;\;\;Q=\frac{I}{\nu}+HH'.
\end{displaymath}](img72.gif) |
(10) |
With these definitions the dual problem (8) becomes
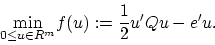 |
(11) |
It will be understood that within the LSVM Algorithm,
the single time that 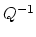 is computed at the outset
of the algorithm, the SMW identity (1) will be used.
Hence only an
is computed at the outset
of the algorithm, the SMW identity (1) will be used.
Hence only an
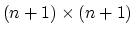 matrix is inverted.
matrix is inverted.
The LSVM Algorithm is based directly on the Karush-Kuhn-Tucker
necessary and sufficient optimality conditions
[15, KTP 7.2.4, page 94] for the dual problem (11):
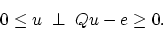 |
(12) |
By using the easily established identity between any two real
numbers (or vectors) 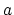 and
and 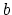 :
:
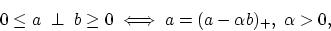 |
(13) |
the optimality condition (12) can be written in the following
equivalent form for any positive 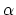 :
:
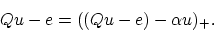 |
(14) |
These optimality conditions lead to the following very simple iterative
scheme which constitutes our LSVM Algorithm:
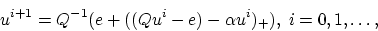 |
(15) |
for which we will establish global linear convergence from any starting
point under the
easily satisfiable condition:
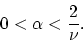 |
(16) |
We impose this condition as
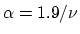 in all our experiments,
where
in all our experiments,
where 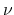 is the parameter of our SVM formulation (7).
It turns out, and this is the way that led us to this
iterative scheme, that the optimality condition (14),
is also the necessary and sufficient condition for the unconstrained minimum of
the implicit Lagrangian [21] associated with the
dual problem (11):
is the parameter of our SVM formulation (7).
It turns out, and this is the way that led us to this
iterative scheme, that the optimality condition (14),
is also the necessary and sufficient condition for the unconstrained minimum of
the implicit Lagrangian [21] associated with the
dual problem (11):
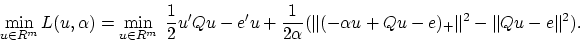 |
(17) |
Setting the gradient with respect to 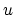 of this convex and differentiable
Lagrangian to zero gives
of this convex and differentiable
Lagrangian to zero gives
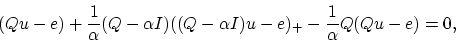 |
(18) |
or equivalently:
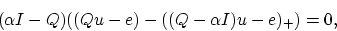 |
(19) |
which is equivalent to the optimality condition (14)
under the assumption that 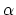 is positive and not an eigenvalue
of
is positive and not an eigenvalue
of 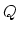 .
.
We establish now the global linear convergence of the iteration (15)
under condition (16).
Algorithm 1
LSVM Algorithm & Its Global Convergence
Let
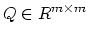
be the symmetric positive
definite matrix defined by (
10) and let (
16) hold. Starting with an arbitrary
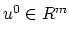
, the iterates
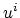
of (
15) converge to the unique solution
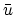
of (
11) at the linear rate:
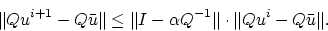 |
(20) |
Proof Because 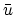 is the solution of (11),
it must satisfy the optimality condition (14) for any
is the solution of (11),
it must satisfy the optimality condition (14) for any 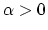 .
Subtracting that equation with
.
Subtracting that equation with 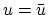 from the iteration
(15) premultiplied by
from the iteration
(15) premultiplied by 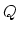 and taking norms gives:
and taking norms gives:
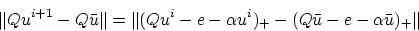 |
(21) |
Using the Projection Theorem [1, Proposition 2.1.3] which
states that the distance between any two points in  is not less than the
distance between their projections on any convex set (the nonnegative orthant
here) in
is not less than the
distance between their projections on any convex set (the nonnegative orthant
here) in  , the above equation gives:
, the above equation gives:
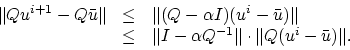 |
(22) |
All we need to show now is that
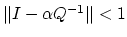 . This follows
from (16) as follows. Noting the definition (10)
of
. This follows
from (16) as follows. Noting the definition (10)
of 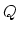 and letting
and letting 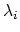 ,
, 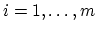 , denote the nonnegative
eigenvalues of
, denote the nonnegative
eigenvalues of 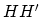 , all we need is:
, all we need is:
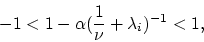 |
(23) |
or equivalently:
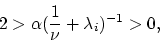 |
(24) |
which is satisfied under the assumption (16).
We give now a complete MATLAB [26] code of LSVM which is
capable of solving problems with millions of points using only native
MATLAB commands.
The input parameters, besides 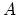 ,
, 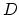 and
and 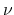 of (10),
which define the problem, are: itmax, the maximum number of iterations
and tol, the tolerated nonzero error in
of (10),
which define the problem, are: itmax, the maximum number of iterations
and tol, the tolerated nonzero error in
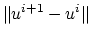 at
termination. The quantity
at
termination. The quantity
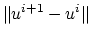 bounds from above:
bounds from above:
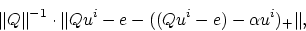 |
(25) |
which measures the violation of the optimality criterion (14).
It follows [20] that
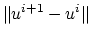 also bounds
also bounds
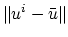 , and by (9) it also bounds
, and by (9) it also bounds
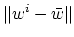 and
and
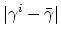 ,
where
,
where
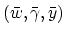 is the unique solution of the primal
SVM (7).
is the unique solution of the primal
SVM (7).
Code 2
LSVM MATLAB M-File
function [it, opt, w, gamma] = svml(A,D,nu,itmax,tol)
% lsvm with SMW for min 1/2*u'*Q*u-e'*u s.t. u=>0,
% Q=I/nu+H*H', H=D[A -e]
% Input: A, D, nu, itmax, tol; Output: it, opt, w, gamma
% [it, opt, w, gamma] = svml(A,D,nu,itmax,tol);
[m,n]=size(A);alpha=1.9/nu;e=ones(m,1);H=D*[A -e];it=0;
S=H*inv((speye(n+1)/nu+H'*H));
u=nu*(1-S*(H'*e));oldu=u+1;
while it<itmax & norm(oldu-u)>tol
z=(1+pl(((u/nu+H*(H'*u))-alpha*u)-1));
oldu=u;
u=nu*(z-S*(H'*z));
it=it+1;
end;
opt=norm(u-oldu);w=A'*D*u;gamma=-e'*D*u;
function pl = pl(x); pl = (abs(x)+x)/2;



Next: 4. LSVM for Nonlinear
Up: Lagrangian Support Vector Machines
Previous: 2. The Linear Support
Journal of Machine Learning Research
![]() ,
, ![]() and
and ![]() of (10),
which define the problem, are: itmax, the maximum number of iterations
and tol, the tolerated nonzero error in
of (10),
which define the problem, are: itmax, the maximum number of iterations
and tol, the tolerated nonzero error in
![]() at
termination. The quantity
at
termination. The quantity
![]() bounds from above:
bounds from above: