


Next: 3. LSVM (Lagrangian Support
Up: Lagrangian Support Vector Machines
Previous: 1. Introduction
2. The Linear Support Vector Machine
We consider the problem of classifying 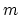 points
in the
points
in the 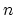 -dimensional real space
-dimensional real space 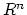 , represented by the
, represented by the
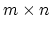 matrix
matrix 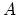 , according to membership
of each point
, according to membership
of each point 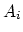 in the class
in the class 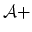 or
or 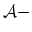 as specified by
a given
as specified by
a given 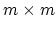 diagonal matrix
diagonal matrix 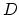 with plus ones or minus ones
along its diagonal. For this problem the standard support
vector machine with a linear kernel [28,4]
is given by the following quadratic program with parameter
with plus ones or minus ones
along its diagonal. For this problem the standard support
vector machine with a linear kernel [28,4]
is given by the following quadratic program with parameter 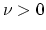 :
:
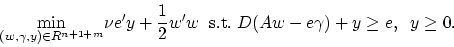 |
(2) |
Here 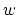 is the normal to the bounding planes:
is the normal to the bounding planes:
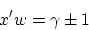 |
(3) |
and 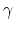 determines their location relative to the origin. See Figure
1.
The plane
determines their location relative to the origin. See Figure
1.
The plane 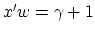 bounds the class
bounds the class 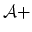 points, possibly with
some error, and the plane
points, possibly with
some error, and the plane 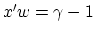 bounds the class
bounds the class 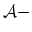 points, also possibly with some error.
The linear separating surface is the plane:
points, also possibly with some error.
The linear separating surface is the plane:
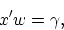 |
(4) |
midway between the bounding planes (3). The quadratic
term in (2) is twice the reciprocal of the square
of the 2-norm distance 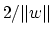 between the two bounding
planes of (3) (see Figure 1). This term
enforces maximization of
this distance, which is often called the ``margin''. If the classes are
linearly inseparable, as depicted in Figure 1, then the two
planes bound the two classes with a ``soft margin''. That is, they
bound each set approximately with some error determined by the
nonnegative error variable
between the two bounding
planes of (3) (see Figure 1). This term
enforces maximization of
this distance, which is often called the ``margin''. If the classes are
linearly inseparable, as depicted in Figure 1, then the two
planes bound the two classes with a ``soft margin''. That is, they
bound each set approximately with some error determined by the
nonnegative error variable 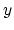 :
:
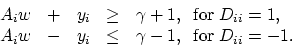 |
(5) |
Traditionally the constant 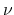 in (2) multiplies
the the 1-norm of the error variable
in (2) multiplies
the the 1-norm of the error variable 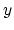 and acts as a weighting
factor. A nonzero
and acts as a weighting
factor. A nonzero 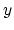 results in an approximate separation as depicted in
Figure 1.
results in an approximate separation as depicted in
Figure 1.
Figure 1:
The bounding planes of a linear SVM with a soft margin
(i.e. with some errors), and the separating plane approximately
separating 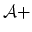 from
from 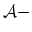 .
.
![\begin{psfrags}
\psfrag{d1}{\Large\OliveGreen{$w$}}
\psfrag{d2}{\Large\OliveGr...
...'w=\gamma $}}
\includegraphics [width=2.2in,angle=0]{margin2c.eps} \end{psfrags}](img59.gif) |
The dual to the standard quadratic linear SVM (2)
[15,25,16,5]
is the following:
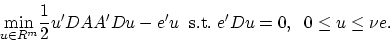 |
(6) |
The variables 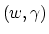 of the primal problem which determine the
separating surface (4) can be obtained from the solution of
the dual problem above [17, Eqns. 5 and 7]. We note
immediately that the matrix
of the primal problem which determine the
separating surface (4) can be obtained from the solution of
the dual problem above [17, Eqns. 5 and 7]. We note
immediately that the matrix 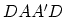 appearing in the dual objective
function (6) is not positive definite in general because
typically
appearing in the dual objective
function (6) is not positive definite in general because
typically 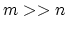 . Also, there is an equality constraint present, in
addition to bound constraints, which for large problems necessitates
special computational procedures such as SMO [24] or
SVM
. Also, there is an equality constraint present, in
addition to bound constraints, which for large problems necessitates
special computational procedures such as SMO [24] or
SVM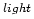 [11]. Furthermore, a one-dimensional
optimization problem [17] must be solved in order to determine
the locator
[11]. Furthermore, a one-dimensional
optimization problem [17] must be solved in order to determine
the locator 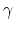 of the separating surface (4). In order
to overcome all these difficulties as well as that of dealing with the
necessity of having to essentially invert a very large matrix of the
order of
of the separating surface (4). In order
to overcome all these difficulties as well as that of dealing with the
necessity of having to essentially invert a very large matrix of the
order of 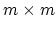 , we propose the following simple but critical
modifications to the standard SVM formulation (2). We change
the 1-norm of
, we propose the following simple but critical
modifications to the standard SVM formulation (2). We change
the 1-norm of 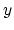 to a 2-norm squared which makes the constraint
to a 2-norm squared which makes the constraint 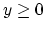 redundant. We also append the term
redundant. We also append the term 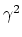 to
to 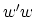 . This in
effect maximizes the margin between the parallel separating planes
(3) by optimizing with respect to both
. This in
effect maximizes the margin between the parallel separating planes
(3) by optimizing with respect to both 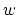 and
and
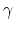 [17], that is with respect to both orientation and
location of the planes, rather that just with respect to
[17], that is with respect to both orientation and
location of the planes, rather that just with respect to 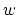 which
merely determines the orientation of the plane. This leads to the
following reformulation of the SVM:
which
merely determines the orientation of the plane. This leads to the
following reformulation of the SVM:
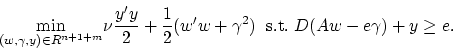 |
(7) |
The dual of this problem is [15]:
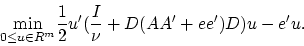 |
(8) |
The variables 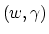 of the primal problem which determine the
separating surface (4) are recovered directly from
the solution of the dual (8) above by the relations:
of the primal problem which determine the
separating surface (4) are recovered directly from
the solution of the dual (8) above by the relations:
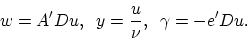 |
(9) |
We immediately note that the matrix appearing in the dual objective function
is positive definite and that there is no equality constraint and no
upper bound on the dual variable 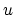 . The only constraint present
is a
nonnegativity one. These facts lead us to our simple
iterative Lagrangian SVM Algorithm which requires the inversion
of a positive definite
. The only constraint present
is a
nonnegativity one. These facts lead us to our simple
iterative Lagrangian SVM Algorithm which requires the inversion
of a positive definite
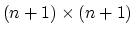 matrix, at the beginning of the algorithm
followed by a straightforward linearly convergent
iterative scheme that requires no optimization package.
matrix, at the beginning of the algorithm
followed by a straightforward linearly convergent
iterative scheme that requires no optimization package.



Next: 3. LSVM (Lagrangian Support
Up: Lagrangian Support Vector Machines
Previous: 1. Introduction
Journal of Machine Learning Research
![\begin{psfrags}
\psfrag{d1}{\Large\OliveGreen{$w$}}
\psfrag{d2}{\Large\OliveGr...
...'w=\gamma $}}
\includegraphics [width=2.2in,angle=0]{margin2c.eps} \end{psfrags}](img59.gif)