Implementation Details

Note that in the algorithm described here, only two steps might be time consuming: the one that computes $\mathcal{W}_i^{'}$ and the one that computes $\boldsymbol{b}_{\mathcal{S}} - \tilde{K}_{\mathcal{S}\mathcal{F}} \boldsymbol{\beta}_{\mathcal{F}}$in (18).

We therefore propose to keep in memory a table of $\mathcal{W}_i^{'}$. Moreover, to update this variable, we can see that

$$\begin{array}{cc} \mbox{for } i \leq l & \mathcal{W}_i^{'\, (... ...lpha_j^{\star \, (t+1)} - \alpha_j^{\star \, (t)} \)\end{array}$$

where

$$S_1 = \{ i, \ \ \alpha_i \in \mathcal{S}\} \ \ \textrm{and} \ \ S_2 = \{ i, \ \ \alpha^{\star}_i \in \mathcal{S}\}.$$

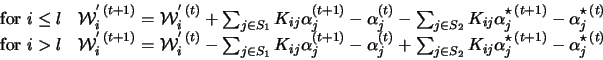
For the computation of $\boldsymbol{b}_{\mathcal{S}} - \tilde{K}_{\mathcal{S}\mathcal{F}} \boldsymbol{\beta}_{\mathcal{F}}$, we can use the following trick:

$$\begin{array}{rcl} \( \boldsymbol{b}_{\mathcal{S}} - \tilde{K... ...thcal{S}} \) _i & \ if \ i > l. \end{array} \right. \end{array}$$

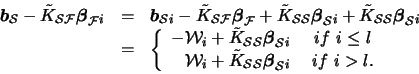
With these two ideas, one can reduce considerably the computational time: instead of computing all the lines of the matrix K, one can compute only the lines corresponding to the variables in $\mathcal{S}$.

Since we only need these lines for the computations, and since it quickly becomes intractable for large problems to keep the whole matrix Kin memory (the size of the matrix being quadratic with respect to the number of examples), it is interesting to implement a cache that keeps in memory the lines of K that corresponds to the most used variables instead of recomputing them at each iteration.