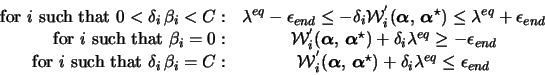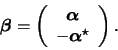Termination Criterion

Given what has been said in the section on shrinking, if we can always have (29) and (30) during the resolution of a subproblem, a reasonable termination criterion is to verify that the $\lambda$ estimated by (31) and (32) verifies the conditions (24)-(28) with a given precision $\epsilon_{end}$.

Thus, we simply verify that

$$\begin{array}{rc} \textrm{for} \ i \ \textrm{such that} \ 0 <... ...r}) + \delta_i \lambda^{eq} \leq \epsilon_{end} \\ \end{array}$$

with $\delta_i = 1$ for $1 \leq i \leq l$, $\delta_i = -1$ for $(l+1) \leq i \leq 2l$ and

$$\boldsymbol{\beta} = \left( \begin{array}{c} \boldsymbol{\alpha} \\ - \boldsymbol{\alpha}^{\star} \end{array}\right).$$