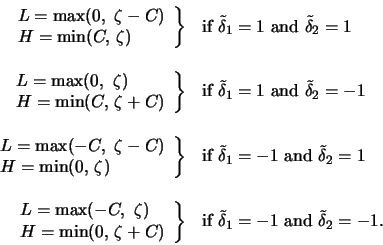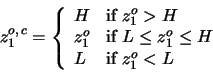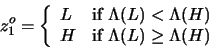We want to solve the problem (3) taking into account
variables
![]() only. To simplify the notation, let us define
only. To simplify the notation, let us define
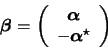
and
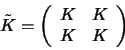
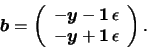
Now let us suppose we can decompose each of the following variables
into two parts (after having reordered the variables accordingly): the first
part corresponds to variables
![]() and the second part
corresponds to the fixed variables
and the second part
corresponds to the fixed variables
![]() :
:
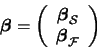
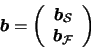
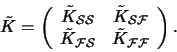
Minimizing (18) under the constraints (19) and (20) can be realized using a constrained
quadratic optimizer, such as a conjugate gradient method with
projection or an interior point method [4].
Moreover, following Platt's idea in SMO [12],
if one fixes the size of the working set
![]() to 2,
the problem can also be solved analytically.
to 2,
the problem can also be solved analytically.
This particular case is important because experimental results show that it always gives the fastest convergence times. We explain it here because it is a different minimization problem from the one proposed by previous authors such as Smola and Schölkopf [14]; in fact, it is easier because it only has 2 variables and not 4.
Let us again simplify the notation:
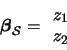
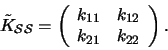
We are searching for a minimum in (21) with respect to z1along the line (22). By inserting (22) into
(21), and after some derivations, it is now equivalent to
minimizing
Let us now consider the constraints (22) and (23).
They force z1 to stay between L and H where