Introduction

Vapnik [15] has proposed a method to solve regression problems using support vector machines. It has yielded excellent performance on many regression and time series prediction problems (see for instance [10] or [2]). This paper proposes an efficient implementation of SVMs for large-scale regression problems. Let us first recall how it works.

Given a training set of l examples $(\boldsymbol{x}_i,\, y_i)$ with $\boldsymbol{x}_i \in E$ and $y_i \in \mathbb{R}$, where E is an Euclidean space with a scalar product denoted $(\ \cdot \ )$, we want to estimate the following linear regression:

$$f(\boldsymbol{x}) = (\boldsymbol{w}\cdot \boldsymbol{x}) + b$$

(with $b \in \mathbb{R}$) with a precision $\epsilon$. For this, we minimize

$$\frac{1}{2}\Vert \boldsymbol{w} \Vert^2 + C \sum_{i=1}^l \vert y_i - f(\boldsymbol{x}_i) \vert _{\epsilon}\;\;,$$

where $\frac{1}{2}\Vert \boldsymbol{w} \Vert^2$ is a regularization factor, C is a fixed constant, and $\vert . \vert _{\epsilon}$ is the $\epsilon$-insensitive loss function defined by Vapnik:

$$\vert z \vert _{\epsilon} = \max\{0, \vert z\vert - \epsilon \}\;\;.$$

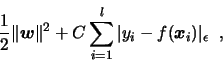
Written as a constrained optimization problem, it amounts to minimizing

$$\tau (\boldsymbol{w},\, \boldsymbol{\xi},\, \boldsymbol{\xi^{... ...\boldsymbol{w} \Vert^2 + C \sum_{i=1}^l (\xi_i + \xi_i^{\star})$$

subject to

$$((\boldsymbol{w}\cdot \boldsymbol{x}_i) + b )- y_i \leq \epsilon + \xi_i$$ (1)

$$y_i - ((\boldsymbol{w}\cdot \boldsymbol{x}_i) + b ) \leq \epsilon + \xi_i^{\star}$$ (2)

$$\xi_i,\, \xi_i^{\star} \geq 0.$$

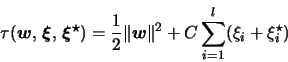
To generalize to non-linear regression, we replace the dot product with a kernel $k(\cdot)$. Then, introducing Lagrange multipliers $\boldsymbol{\alpha}$ and $\boldsymbol{\alpha}^{\star}$, the optimization problem can be stated as:

Minimize the objective function

$$\mathcal{W}(\boldsymbol{\alpha}, \, \boldsymbol{\alpha}^{\sta... ...oldsymbol{\alpha})^{\raisebox{2pt}{\tiny T}} \, \boldsymbol{1}$$ (3)

subject to

$$(\boldsymbol{\alpha}-\boldsymbol{\alpha}^{\star})^{\raisebox{2pt}{\tiny T}} \, \boldsymbol{1} = 0$$ (4)

and

$$0 \leq \alpha^{\star}_i, \ \alpha_i \leq C, \ \ \ i = 1 ... l$$ (5)

where 1 is the unit vector and K is the matrix with coefficients $K_{ij} = k(\boldsymbol{x}_i,\, \boldsymbol{x}_j)$. The estimate of the regression function at a given point is then

$$f(\boldsymbol{x}) = \sum_{i=1}^l (\alpha_i^{\star} - \alpha_i) k(\boldsymbol{x}_i,\, \boldsymbol{x}) + b$$

where b is computed using the fact that (1) becomes an equality with $\xi_i = 0$ if $0 < \alpha_i < C$and (2) becomes an equality with $\xi_i^{\star} = 0$ if $0 < \alpha_i^{\star} < C$.

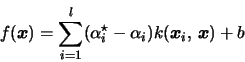
Solving the minimization problem (3) under the constraints (4) and (5) needs resources on the order of l² and is thus difficult for problems with large l.

In this paper, we propose a method to solve such problems efficiently using a decomposition algorithm similar to the one proposed by Joachims [5] in the context of classification problems. In the next section, we give the general algorithm and explain in more detail each of its main steps and how they differ from other published algorithms, as well as a discussion on convergence and on some important implementation issues, such as a way to efficiently handle the kernel matrix computation. In the experiment section, we compare this new algorithm on small and large datasets to Nodelib, another SVM algorithm for large-scale regression problems proposed by Flake and Lawrence [3], then show how the size of the internal memory allocated to the resolution of the problem is related to the time needed to solve it, and finally how our algorithm scales with respect to l.