


Next: Categorization of Adjuncts
Up: The Categorization Process
Previous: The Categorization Process
The context used to find out the nuclei relies on this simple following observation: A structure requires at least one nucleus4.
The pattern used in order to determine nuclei is:
![$\displaystyle f\raisebox{-5pt}{\footnotesize char}(X)= \frac{\sum_{C}{[X]}}{\sum_{C}{X}}$](img26.png) |
|
|
(1) |
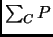 corresponds to the number of occurrences of the pattern P in the corpus
corresponds to the number of occurrences of the pattern P in the corpus 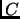 .
The brackets are used in order to delimit the structure (NP for example).
.
The brackets are used in order to delimit the structure (NP for example).
 PRP
PRP ![$]$](img30.png) means that the structure is composed of only one word tagged PRP.
Elements that occur alone in a structure are assimilated to nucleus, since a structure requires a nucleus.
For example, the tags PRP (pronoun) and NNP (proper noun) may compose alone a structure (respectively 99% and 48% of these tags appear alone in NP) but the tag JJ appears rarely alone (0.009%).
A threshold tuned empirically is used in order to discriminate nuclei from adjuncts.
We deduce that PRP and NNP belong to the nuclei and not JJ.
But this criterion does not allow the identification of all the nuclei.
Some often appear with adjuncts (an English noun (NN) often5 occurs with a determiner or an adjective and thus appears alone only 13%).
The single use of this characteristic provides a continuum of values where the automatic set up of a threshold between adjuncts and nuclei is problematic and depends on the structure.
To solve this problem, the categorization of nuclei is decomposed into two steps.
First we identify characteristic adjuncts, i.e. adjuncts which can not appear alone since they depend on a nucleus.
An effect of the function
means that the structure is composed of only one word tagged PRP.
Elements that occur alone in a structure are assimilated to nucleus, since a structure requires a nucleus.
For example, the tags PRP (pronoun) and NNP (proper noun) may compose alone a structure (respectively 99% and 48% of these tags appear alone in NP) but the tag JJ appears rarely alone (0.009%).
A threshold tuned empirically is used in order to discriminate nuclei from adjuncts.
We deduce that PRP and NNP belong to the nuclei and not JJ.
But this criterion does not allow the identification of all the nuclei.
Some often appear with adjuncts (an English noun (NN) often5 occurs with a determiner or an adjective and thus appears alone only 13%).
The single use of this characteristic provides a continuum of values where the automatic set up of a threshold between adjuncts and nuclei is problematic and depends on the structure.
To solve this problem, the categorization of nuclei is decomposed into two steps.
First we identify characteristic adjuncts, i.e. adjuncts which can not appear alone since they depend on a nucleus.
An effect of the function
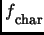 is to provide a very small value for adjuncts.
If the value of an element is lower than a given threshold (
is to provide a very small value for adjuncts.
If the value of an element is lower than a given threshold (
 ), then it is categorized as a characteristic adjunct.
The same function is used for determining nuclei and adjuncts.
In the first case, the function has to be greater than a given threshold, in the second case, lesser than a given second threshold.
For example the number of occurrences in the training corpus of the pattern
), then it is categorized as a characteristic adjunct.
The same function is used for determining nuclei and adjuncts.
In the first case, the function has to be greater than a given threshold, in the second case, lesser than a given second threshold.
For example the number of occurrences in the training corpus of the pattern ![$[ JJ ]$](img33.png) is 99, and the number of occurrences of the pattern
is 99, and the number of occurrences of the pattern 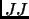 (including the pattern [ JJ ]) is 11097.
So
(including the pattern [ JJ ]) is 11097.
So
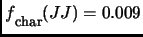 , value being low enough to consider JJ as a characteristic adjunct.
The list provided by
, value being low enough to consider JJ as a characteristic adjunct.
The list provided by
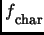 for English NP is:
These elements can correspond to left or right adjuncts.
All the adjuncts are not identified, but this list allows the identification of the nuclei.
for English NP is:
These elements can correspond to left or right adjuncts.
All the adjuncts are not identified, but this list allows the identification of the nuclei.
The second step consists in introducing these elements into a new pattern used by the function
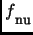 .
This pattern matches elements surrounded by these characteristic adjuncts.
It thus matches nuclei which often appear with adjuncts.
Since a sequence of adjuncts (as an adjunct alone) can not alone compose a complete structure,
.
This pattern matches elements surrounded by these characteristic adjuncts.
It thus matches nuclei which often appear with adjuncts.
Since a sequence of adjuncts (as an adjunct alone) can not alone compose a complete structure, 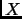 only matches elements which correspond to a nucleus.
only matches elements which correspond to a nucleus.
![$\displaystyle f\raisebox{-5pt}{\footnotesize nu}(X)=\frac{\sum_{C}{[\
A\raiseb...
...size {char}}* X \
A\raisebox{-5pt}{\footnotesize {char}}*\
]}}{\sum_{C}{X}}$](img40.png) |
|
|
(2) |
The function
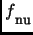 is a good discrimination function between nuclei and adjuncts and provides very low values for adjuncts and very high values for nuclei (Table 7).
is a good discrimination function between nuclei and adjuncts and provides very low values for adjuncts and very high values for nuclei (Table 7).
Table 7:
Detection of some nuclei of the English NP (nouns and pronouns).
| x |
Freq(x) |
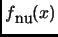 |
nucleus |
| POS |
1759 |
0.00 |
no |
| PRP$ |
1876 |
0.01 |
no |
| JJ |
11097 |
0.02 |
no |
| DT |
18097 |
0.03 |
no |
| RB |
919 |
0.06 |
no |
| NNP |
11046 |
0.74 |
yes |
| NN |
21240 |
0.87 |
yes |
| NNPS |
164 |
0.93 |
yes |
| NNS |
7774 |
0.95 |
yes |
| WP |
527 |
0.97 |
yes |
| PRP |
3800 |
0.99 |
yes |
|



Next: Categorization of Adjuncts
Up: The Categorization Process
Previous: The Categorization Process
Hammerton J.
2002-03-13
![$\displaystyle f\raisebox{-5pt}{\footnotesize char}(X)= \frac{\sum_{C}{[X]}}{\sum_{C}{X}}$](img26.png)
![$\displaystyle f\raisebox{-5pt}{\footnotesize char}(X)= \frac{\sum_{C}{[X]}}{\sum_{C}{X}}$](img26.png)
![]() .
This pattern matches elements surrounded by these characteristic adjuncts.
It thus matches nuclei which often appear with adjuncts.
Since a sequence of adjuncts (as an adjunct alone) can not alone compose a complete structure,
.
This pattern matches elements surrounded by these characteristic adjuncts.
It thus matches nuclei which often appear with adjuncts.
Since a sequence of adjuncts (as an adjunct alone) can not alone compose a complete structure, ![]() only matches elements which correspond to a nucleus.
only matches elements which correspond to a nucleus.
![$\displaystyle f\raisebox{-5pt}{\footnotesize nu}(X)=\frac{\sum_{C}{[\
A\raiseb...
...size {char}}* X \
A\raisebox{-5pt}{\footnotesize {char}}*\
]}}{\sum_{C}{X}}$](img40.png)
![]() is a good discrimination function between nuclei and adjuncts and provides very low values for adjuncts and very high values for nuclei (Table 7).
is a good discrimination function between nuclei and adjuncts and provides very low values for adjuncts and very high values for nuclei (Table 7).