Selection of a New Working Set

We propose to select a new set of q variables such that the overall criterion will be optimized. In order to select such a working set, we use the same idea as Joachims [5]: simply search for the optimal gradient-descent direction p which is feasible and which has only q non-null components. The variables corresponding to these components are chosen to be the new working set $\mathcal{S}$.

We thus need to minimize:

$$\mathcal{V}(\boldsymbol{p}) = \left( \mathcal{W}^{'}(\boldsym... ...}^{\star}) \right)^{\raisebox{2pt}{\tiny T}} \, \boldsymbol{p}$$ (6)

with

$$\boldsymbol{p} = ( d_1 \ldots d_l, \, d^{\star}_1 \ldots d^{\star}_l )^{\raisebox{2pt}{\tiny T}}$$

subject to:

$$\boldsymbol{1}^{\raisebox{2pt}{\tiny T}} \, \boldsymbol{d} - ... ...bol{1}^{\raisebox{2pt}{\tiny T}} \, \boldsymbol{d}^{\star} = 0$$ (7)

$$\begin{array}{ccl} d_i \geq 0 & \ \mathrm{for} \ & i \ \mathr... ...\ & i \ \mathrm{such \ that} \ \alpha_i^{\star} = C \end{array}$$ (8)

and

$$-\,\boldsymbol{1} \ \leq \ \boldsymbol{p} \ \leq \ \boldsymbol{1}$$ (9)

$$\mathrm{card}\{ p_i \ : \ p_i \neq 0 \} = q.$$ (10)

Since we are searching for an optimal descent direction, which is a direction where the scalar product with the gradient is the smallest, we want indeed to minimize (6). The conditions (7) and (8) are necessary to ensure the feasibility of the obtained direction. The condition (9) is there only to ensure that the problem has a solution. Finally, (10) is imposed because we are searching for a direction with only q non-null components.

Note that the derivative of $\mathcal{W}$ can be easily computed:

$$\mathcal{W}^{'}(\boldsymbol{\alpha},\, \boldsymbol{\alpha}^{\... ... - \boldsymbol{y} + \boldsymbol{1}\, \epsilon \end{array}\) .$$

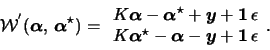
In order to solve this problem, it thus suffices to consider

$$\omega_i = \delta_i \, \mathcal{W}^{'}_i\;\;,$$

where $\delta_i = 1$ for $1 \leq i \leq l$ and $\delta_i = -1$ for $l+1 \leq i \leq 2l$. To simplify, let q be even, and let us sort the $\omega_i$ in decreasing order. Let us then denote $\varphi$ as the bijection of $\{1\ldots2l\}$ into itself such that the $\omega_{\varphi(i)}$ are sorted. Let us then select the q/2 first indices $\varphi(i)$ such that:

$$\mbox{if } \varphi(i) \leq l, \mbox{ we have } 0 < \alpha_{\varphi(i)} \leq C$$

$$\mbox{if } \varphi(i) > l, \mbox{ we have } 0 \leq \alpha^{\star}_{\varphi(i)-l} < C\;\;;$$

and let us select also the q/2 last indices $\varphi(i)$ such that:

$$\mbox{if } \varphi(i) \leq l, \mbox{ we have } 0 \leq \alpha_{\varphi(i)} < C$$

$$\mbox{if } \varphi(i) > l, \mbox{ we have } 0 < \alpha^{\star}_{\varphi(i)-l} \leq C.$$

Since we are searching for exactly q variables, the $\varphi(i)$ must be distinct. We could have to reduce q if one variable is selected twice.

Lemma 1   Let us now denote $c_i, \ i = 1 \ldots q$, the q indices we just chose, then the direction $\rho$ such that

$$\rho_j = \left\{\begin{array}{l} -\delta_j \mbox{ \emph{if} }... ...ldots c_{q}\} \\ 0 \mbox{ \emph{otherwise}} \end{array}\right.$$

is a solution of the minimization problem (6).

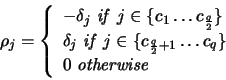
Proof: Let us go back to the minimization problem of the function

$$(z_1,\, \ldots\, z_{2l}) \longmapsto \sum_{i=1\ldots 2l}\omega_i \, z_i$$ (11)

subject to

$$\sum_i z_i = 0$$ (12)

$$-1 \leq z_i \leq 1$$ (13)

and

$$\textrm{card} \{z_i, \, z_i \not= 0 \} = q$$ (14)

with $z_i = \delta_i p_i$. (The reasoning is the same if we take the constraints (8) into account).

In the case where 2l = q = 2r, it is easy to see that the minimum is obtained for z_i = -1 if $i = 1\ldots r$ and z_i = 1 if $i = r+1\ldots q$: if for instance z_i0 is augmented by $\gamma \geq 0$ for a $i_0 \leq r$, then one needs to compensate by $-\gamma$ another z_j to maintain (12). Since we want to minimize (11), the best thing to do, knowing that the $\omega_i$ are sorted in reverse order and keeping in mind the constraint (13), is to modify z_q and thus to fix $z_q = 1-\gamma$. Equation (11) is then augmented by $(\omega_{i_0}-\omega_q) \gamma$, which is a positive value because the $\omega_i$ are sorted and thus we get out of the minimum.

In the case where 2l > q = 2r, suppose we found a z which is a solution of (11). Let us denote $k_1\ldots k_q$ the q indices of the components of z which are non-null. Using the same argument as in the previous paragraph, it is clear that $z_{k_1}\ldots z_{k_r} = -1$ and that $z_{k_r+1}\ldots z_{k_q} = 1$. In other words, if z is a solution of our problem, then we necessarily have $z_{k_i} = \pm 1$. Considering again the order of the $\omega_i$, it becomes evident that we have to take $(k_1=1)\ldots (k_r = r)$ and $(k_{r+1}=2l-r)\ldots (k_q = 2l)$.
$\square$

Our new working set $\mathcal{S}$ is then composed of the q variables corresponding to the indices c_i (where an index $c_i \leq l$ corresponds to $\alpha_{c_i}$ and an index c_i > l corresponds to $\alpha^{\star}_{c_i-l}$).