The ultimate goal of decision making is to find an optimal
behavior subject to some optimality criterion. Optimizing for the
infinite-horizon expected discounted total reward is one of the
most studied such criteria. Under this criterion, we are trying to
find a policy that maximizes the expected value of
![]() , where
, where ![]() is the immediate
reward in time step
is the immediate
reward in time step ![]() and
and
![]() is the discount
factor.
is the discount
factor.
A standard way to find an optimal policy is to compute the optimal
value function
![]() , which gives the value of each
state (the expected cumulated discounted reward with the given
starting state). From this, the optimal policy can be easily
obtained: the `greedy' policy with respect to the optimal value
function is an optimal policy (see e.g.
[Sutton and Barto(1998)]). This is the well-known
value-function approach [Bellman(1957)].
, which gives the value of each
state (the expected cumulated discounted reward with the given
starting state). From this, the optimal policy can be easily
obtained: the `greedy' policy with respect to the optimal value
function is an optimal policy (see e.g.
[Sutton and Barto(1998)]). This is the well-known
value-function approach [Bellman(1957)].
Formally, the optimal value function satisfies the following recursive system of equations known as Bellman equations [Bellman(1957)]:
Besides the state-value function, some other types of value
functions can be defined as well. One example is the
state-action-value function
![]() , which
satisfies
, which
satisfies
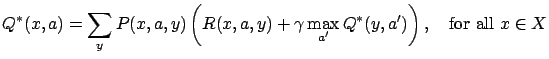 |
in the optimal case. ![]() has the meaning ``the
expected value of taking action
has the meaning ``the
expected value of taking action ![]() in state
in state ![]() while following
the optimal policy''. Here the values of state-action pairs are
learned instead of state values, which enables model-free learning
[Watkins(1989)]. The corresponding learning algorithm is
called Q-learning.
while following
the optimal policy''. Here the values of state-action pairs are
learned instead of state values, which enables model-free learning
[Watkins(1989)]. The corresponding learning algorithm is
called Q-learning.
It is well known that for
![]() , Equation 1
has a unique solution. The Bellman equations can be rewritten
using operators:
, Equation 1
has a unique solution. The Bellman equations can be rewritten
using operators: ![]() is the (unique) fixed point of
operator
is the (unique) fixed point of
operator ![]() (called the dynamic programming operator),
where
(called the dynamic programming operator),
where
 = \max_a \sum_y P(x,a,y) \left( R(x,a,y) + \gamma V(y) \right).$](img32.gif) |