Similarly to most other RL algorithms, the E-learning algorithm
[Lorincz et al.(2002)] also uses a value function, the
event-value function
![]() . Pairs of
states
. Pairs of
states ![]() and
and ![]() are called events and
desired events, respectively. For a given initial state
are called events and
desired events, respectively. For a given initial state
![]() , let us denote the desired next state by
, let us denote the desired next state by ![]() . The
. The
![]() state sequence is the desired event, or
subtask,
state sequence is the desired event, or
subtask, ![]() is the value of trying to get from
actual state
is the value of trying to get from
actual state ![]() to next state
to next state ![]() . State
. State ![]() reached by the
subtask could be different from the desired state
reached by the
subtask could be different from the desired state ![]() . One of
the advantages of this formulation is that one may--but does not
have to--specify the transition time: Realizing the subtask may
take more than one step for the controller, which is working in
the background.
. One of
the advantages of this formulation is that one may--but does not
have to--specify the transition time: Realizing the subtask may
take more than one step for the controller, which is working in
the background.
This value may be different from the expected discounted total reward of eventually
getting from ![]() to
to ![]() . We use the former definition, since we want to use the
event-value function for finding an optimal successor state. To this end, the
event-selection policy
. We use the former definition, since we want to use the
event-value function for finding an optimal successor state. To this end, the
event-selection policy
![]() is introduced.
is introduced.
![]() gives the probability of selecting desired state
gives the probability of selecting desired state ![]() in state
in state ![]() . However, the system
usually cannot be controlled by ``wishes" (desired new states);
decisions have to be
expressed in actions. This is done by the action-selection policy (or controller policy)
. However, the system
usually cannot be controlled by ``wishes" (desired new states);
decisions have to be
expressed in actions. This is done by the action-selection policy (or controller policy)
![]() , where
, where
![]() gives the probability
that the agent selects action
gives the probability
that the agent selects action ![]() to realize the transition
to realize the transition ![]() .4
.4
An important property of event learning is the following: only the event-selection policy is learned (through the event-value function) and the learning problem of the controller's policy is separated from E-learning. From the viewpoint of E-learning, the controller policy is part of the environment, just like the transition probabilities.
The event-value function corresponding to a given action selection policy can be expressed by the state value function:
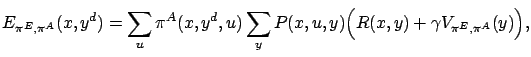 |
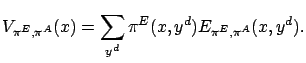 |
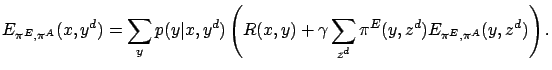 |
It can be shown that
![]() satisfies the following
Bellman-type equations:
satisfies the following
Bellman-type equations:
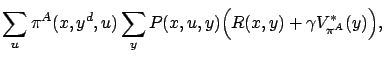 where where |
|||
An optimal event-value function with respect to an optimal
controller policy will be denoted by ![]() .
.