


Next: Learning of tree distributions
Up: Tree distributions
Previous: Marginalization, inference and sampling
Representational capabilities
If graphical representations are natural for human intuition,
then the subclass of tree models are particularly intuitive.
Trees are sparse graphs, having 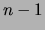 or fewer edges. There is
at most one path between every pair of variables; thus,
independence relationships between subsets of variables, which are
not easy to read out in general Bayesian network topologies, are
obvious in a tree. In a tree, an edge corresponds to the
simple, common-sense notion of direct dependency and is the natural
representation for it. However, the very simplicity that makes tree
models appealing also limits their modeling power. Note
that the number of free parameters in a tree grows linearly
with
or fewer edges. There is
at most one path between every pair of variables; thus,
independence relationships between subsets of variables, which are
not easy to read out in general Bayesian network topologies, are
obvious in a tree. In a tree, an edge corresponds to the
simple, common-sense notion of direct dependency and is the natural
representation for it. However, the very simplicity that makes tree
models appealing also limits their modeling power. Note
that the number of free parameters in a tree grows linearly
with 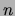 while the size of the state space
while the size of the state space 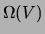 is an
exponential function of
is an
exponential function of 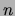 . Thus the class of dependency
structures representable by trees is a relatively small one.
. Thus the class of dependency
structures representable by trees is a relatively small one.
Journal of Machine Learning Research
2000-10-19