

Next: Conclusions
Up: The accelerated tree learning
Previous: Presorting mutual information values
Experiments
In this section we report on the results of experiments that
compare the speed of the ACCL algorithm with the standard
CHOWLIU method on artificial data.
In our experiments the binary domain dimension 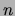 varies from
varies from
 to
to  . Each data point has a fixed number
. Each data point has a fixed number 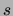 of variables
taking value 1. The sparseness
of variables
taking value 1. The sparseness 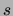 takes the values 5, 10,
15 and 100. The data were generated from an artificially constructed
non-uniform, non-factored distribution. For each pair
takes the values 5, 10,
15 and 100. The data were generated from an artificially constructed
non-uniform, non-factored distribution. For each pair 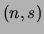 a set of
10,000 points was created.
For each data set both the CHOWLIU algorithm and the ACCL
algorithm were used to fit a single tree distribution. The running times
are plotted in Figure 23. The improvements of ACCL
over the standard version are spectacular: learning a tree on 1000 variables
from 10,000 data points takes 4 hours with the standard algorithm and
only 4 seconds with the accelerated version when the data are sparse
(
a set of
10,000 points was created.
For each data set both the CHOWLIU algorithm and the ACCL
algorithm were used to fit a single tree distribution. The running times
are plotted in Figure 23. The improvements of ACCL
over the standard version are spectacular: learning a tree on 1000 variables
from 10,000 data points takes 4 hours with the standard algorithm and
only 4 seconds with the accelerated version when the data are sparse
(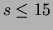 ). For the less sparse regime of
). For the less sparse regime of 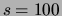 the ACCL
algorithm takes 2 minutes to complete, improving on the traditional
algorithm by a factor of 120.
Note also that the running time of the accelerated algorithm seems
to be nearly independent of the dimension of the domain.
Recall on the other hand that the number of steps
the ACCL
algorithm takes 2 minutes to complete, improving on the traditional
algorithm by a factor of 120.
Note also that the running time of the accelerated algorithm seems
to be nearly independent of the dimension of the domain.
Recall on the other hand that the number of steps 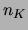 (Figure
24) grows with
(Figure
24) grows with 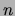 . This implies that the
bulk of the computation lies in the steps preceding the Kruskal
algorithm proper. Namely, it is in the computing of co-occurrences and
organizing the data that most of the time is spent. Figure
23 also confirms that the running time of the
traditional CHOWLIU algorithm grows quadratically with
. This implies that the
bulk of the computation lies in the steps preceding the Kruskal
algorithm proper. Namely, it is in the computing of co-occurrences and
organizing the data that most of the time is spent. Figure
23 also confirms that the running time of the
traditional CHOWLIU algorithm grows quadratically with 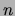 and
is independent of
and
is independent of 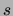 .
This concludes the presentation of the ACCL algorithm. The
method achieves its performance gains by exploiting characteristics of the
data (sparseness) and of the problem (the weights represent mutual
information) that are external to the maximum weight spanning tree
algorithm proper. The algorithm obtained is worst case
.
This concludes the presentation of the ACCL algorithm. The
method achieves its performance gains by exploiting characteristics of the
data (sparseness) and of the problem (the weights represent mutual
information) that are external to the maximum weight spanning tree
algorithm proper. The algorithm obtained is worst case
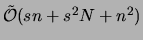 but typically
but typically
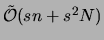 ,
which represents a significant asymptotic improvement over the
,
which represents a significant asymptotic improvement over the
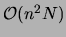 of the traditional Chow and Liu algorithm.
Moreover, if
of the traditional Chow and Liu algorithm.
Moreover, if 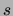 is large, then the ACCL algorithm
(gracefully) degrades to the standard CHOWLIU algorithm.
The algorithm extends to non-integer counts, hence being directly
applicable to mixtures of trees. As we have seen empirically, a
very significant part of the running time is spent in computing
co-occurrences. This prompts future work on learning statistical
models over large domains that focus on the efficient computation
and usage of the relevant sufficient statistics. Work in this direction
includes the structural EM algorithm [Friedman 1998,Friedman, Getoor 1999]
as well as A-D trees [Moore, Lee 1998]. The latter are closely related to our
representation of the pairwise marginals
is large, then the ACCL algorithm
(gracefully) degrades to the standard CHOWLIU algorithm.
The algorithm extends to non-integer counts, hence being directly
applicable to mixtures of trees. As we have seen empirically, a
very significant part of the running time is spent in computing
co-occurrences. This prompts future work on learning statistical
models over large domains that focus on the efficient computation
and usage of the relevant sufficient statistics. Work in this direction
includes the structural EM algorithm [Friedman 1998,Friedman, Getoor 1999]
as well as A-D trees [Moore, Lee 1998]. The latter are closely related to our
representation of the pairwise marginals 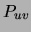 by counts. In fact,
our representation can be viewed as a ``reduced'' A-D tree that stores
only pairwise statistics. Consequently, when an A-D tree
representation is already computed, it can be exploited in steps 1 and
2 of the ACCL algorithm. Other versions of the
ACCL algorithm are discussed by THESIS.
by counts. In fact,
our representation can be viewed as a ``reduced'' A-D tree that stores
only pairwise statistics. Consequently, when an A-D tree
representation is already computed, it can be exploited in steps 1 and
2 of the ACCL algorithm. Other versions of the
ACCL algorithm are discussed by THESIS.


Next: Conclusions
Up: The accelerated tree learning
Previous: Presorting mutual information values
Journal of Machine Learning Research
2000-10-19