


Next: The SPLICE dataset: Structure
Up: Classification with mixtures of
Previous: The NURSERY dataset
We also studied the classification performance of the MT model
in the domain of DNA SPLICE-junctions. The domain consists
of 60 variables, representing a sequence of DNA bases, and an
additional class variable [Rasmussen
1996]. The task is to determine if
the middle of the sequence is a splice junction and what is its
type. Splice junctions are of two types: exon-intron (EI) represents
the end of an exon and the beginning of an intron whereas intron-exon
(IE) is the place where the intron ends and the next exon, or coding
section, begins. Hence, the class variable can take 3 values
(EI, IE or no junction) and the other variables take 4 values
corresponding to the 4 possible DNA bases (C, A, G, T).
The dataset consists of 3,175 labeled examples.2
We ran two series of experiments comparing the MT model with competing
models. In the first series of experiments, we compared to the
results of noordewier:91, who used multilayer neural networks
and knowledge-based neural networks for the same task. We replicated
these authors' choice of training set size (2000) and test set size
(1175) and sampled new training/test sets for each trial. We
constructed trees ( ) and mixtures of trees (
) and mixtures of trees ( ). In fitting
the mixture, we used an early-stopping procedure in which
). In fitting
the mixture, we used an early-stopping procedure in which
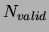 =300 examples were separated out of the training set and
training was stopped when the likelihood on these examples stopped
increasing. The results, averaged over 20 trials, are presented in
Figure 15 for a variety of values of
=300 examples were separated out of the training set and
training was stopped when the likelihood on these examples stopped
increasing. The results, averaged over 20 trials, are presented in
Figure 15 for a variety of values of
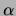 . It can be seen that the single tree and the MT model perform
similarly, with the single tree showing an insignificantly better
classification accuracy. Note that in this situation smoothing does
not improve performance; this is not unexpected since the data set is
relatively large. With the exception of the ``oversmoothed'' MT model
(
. It can be seen that the single tree and the MT model perform
similarly, with the single tree showing an insignificantly better
classification accuracy. Note that in this situation smoothing does
not improve performance; this is not unexpected since the data set is
relatively large. With the exception of the ``oversmoothed'' MT model
(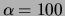 ), all the single tree or MT models outperform the other
models tested on this problem. Note that whereas the tree models
contain no prior knowledge about the domain, the other two models do:
the neural network model is trained in supervised mode, optimizing for
class accuracy, and the KBNN includes detailed domain knowledge.
Based on the strong showing of the single tree model on the SPLICE
task, we pursued a second series of experiments in which we compare
the tree model with a larger collection of methods from the DELVE
repository [Rasmussen,
1996]. The DELVE benchmark uses subsets of the
SPLICE database with 100 and 200 examples for training. Testing is
done on 1500 examples in all cases. Figure 16
presents the results for the algorithms tested by DELVE as well
as the single trees with different degrees of smoothing. We also
show results for naive Bayes (NB) and Tree Augmented Naive Bayes
(TANB) models [Friedman, Geiger, Goldszmidt
1997]. The results from DELVE represent
averages over 20 runs with different random initializations on the
same training and testing sets; for trees, NB and TANB, whose outputs are
not initialization-dependent, we averaged the performance of the models
learned for 20 different splits of the union of the training and
testing set. No early stopping or cross-validation was used in this case.
), all the single tree or MT models outperform the other
models tested on this problem. Note that whereas the tree models
contain no prior knowledge about the domain, the other two models do:
the neural network model is trained in supervised mode, optimizing for
class accuracy, and the KBNN includes detailed domain knowledge.
Based on the strong showing of the single tree model on the SPLICE
task, we pursued a second series of experiments in which we compare
the tree model with a larger collection of methods from the DELVE
repository [Rasmussen,
1996]. The DELVE benchmark uses subsets of the
SPLICE database with 100 and 200 examples for training. Testing is
done on 1500 examples in all cases. Figure 16
presents the results for the algorithms tested by DELVE as well
as the single trees with different degrees of smoothing. We also
show results for naive Bayes (NB) and Tree Augmented Naive Bayes
(TANB) models [Friedman, Geiger, Goldszmidt
1997]. The results from DELVE represent
averages over 20 runs with different random initializations on the
same training and testing sets; for trees, NB and TANB, whose outputs are
not initialization-dependent, we averaged the performance of the models
learned for 20 different splits of the union of the training and
testing set. No early stopping or cross-validation was used in this case.
Figure 17:
Cumulative adjacency matrix of 20
trees fit to 2000 examples of the SPLICE data set with no
smoothing. The size of the square at coordinates 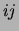 represents the
number of trees (out of 20) that have an edge between variables
represents the
number of trees (out of 20) that have an edge between variables  and
and  . No square means that this number is 0. Only the lower half
of the matrix is shown. The class is variable 0. The group of squares
at the bottom of the figure shows the variables that are connected
directly to the class. Only these variable are relevant for
classification. Not surprisingly, they are all located in the
vicinity of the splice junction (which is between 30 and 31). The
subdiagonal ``chain'' shows that the rest of the variables
are connected to their immediate neighbors. Its lower-left end is
edge 2-1 and its upper-right is edge 60-59.
. No square means that this number is 0. Only the lower half
of the matrix is shown. The class is variable 0. The group of squares
at the bottom of the figure shows the variables that are connected
directly to the class. Only these variable are relevant for
classification. Not surprisingly, they are all located in the
vicinity of the splice junction (which is between 30 and 31). The
subdiagonal ``chain'' shows that the rest of the variables
are connected to their immediate neighbors. Its lower-left end is
edge 2-1 and its upper-right is edge 60-59.
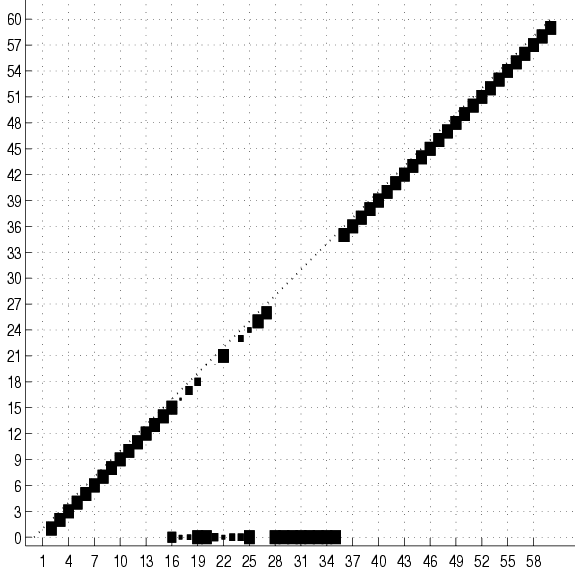 |
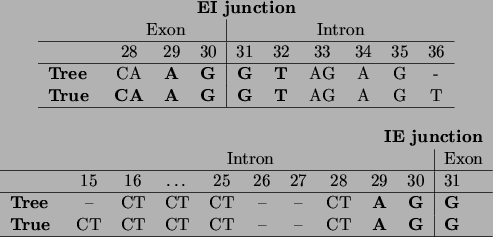
Figure 18:
The encoding of the IE and EI splice junctions as discovered by the
tree learning algorithm, compared to the ones given by Watson
et al., ``Molecular Biology of the Gene'' [Watson, Hopkins, Roberts, Steitz,
Weiner 1987].
Positions in the sequence are consistent with our variable numbering: thus
the splice junction is situated between positions 30 and 31. Symbols in
boldface indicate bases that are present with probability almost 1,
other A,C,G,T symbols indicate bases or groups of bases that have high
probability ( 0.8), and a - indicates that the position can be
occupied by any base with a non-negligible probability.
0.8), and a - indicates that the position can be
occupied by any base with a non-negligible probability.
 |
The results show that the single tree is quite successful in this
domain, yielding an error rate that is less than half of the error
rate of the best model tested in DELVE. Moreover, the average error of
a single tree trained on 200 examples is 6.9%, which is only 2.3%
greater than the average error of the tree trained on 2000
examples. We attempt to explain this striking
preservation of accuracy for small training sets
in our discussion of feature selection in
Section 5.3.7.
The Naive Bayes model exhibits behavior that is very similar to
the tree model and only slightly less accurate. However, augmenting
the Naive Bayes model to a TANB significantly hurts the classification
performance.
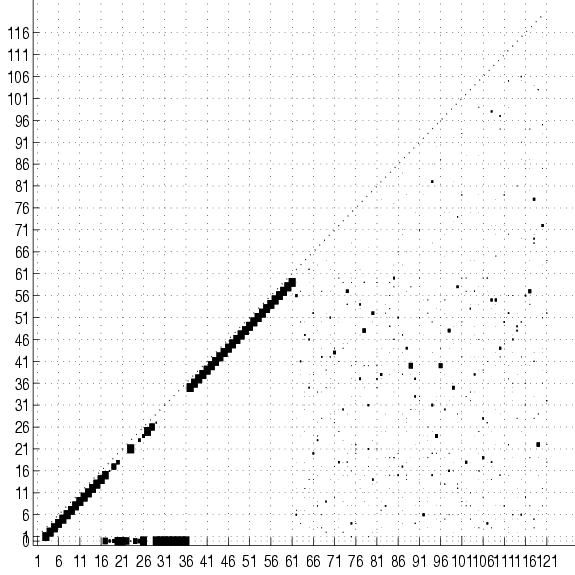
Figure 19:
The cumulated adjacency matrix for
20 trees over the original set of variables (0-60) augmented with 60
``noisy'' variables (61-120) that are independent of the original ones. The
matrix shows that the tree structure over the original variables is
preserved.
 |



Next: The SPLICE dataset: Structure
Up: Classification with mixtures of
Previous: The NURSERY dataset
Journal of Machine Learning Research
2000-10-19



