

Next: Q-learning in Generalized -MDPs
Up: MDPs in Varying Environments
Previous: Generalized -MDPs
Asymptotic Boundedness of Value Iteration
In this section we prove a generalized form of the convergence
theorem of Szepesvári and Littman's (for the original theorem, see
Appendix A). We do not require probability one
uniform convergence of the approximating operators, but only a
sufficiently close approximation. Therefore the theorem can be
applied to prove results about algorithms in generalized
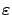 -MDPs.
Our definition of closeness both for value functions and
dynamic-programming operators is given below.
-MDPs.
Our definition of closeness both for value functions and
dynamic-programming operators is given below.
Let 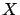 be an arbitrary state space and denote by
be an arbitrary state space and denote by
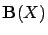 the set of value functions. Let
the set of value functions. Let
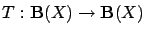 be an arbitrary contraction mapping with unique
fixed point
be an arbitrary contraction mapping with unique
fixed point 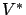 , and let
, and let
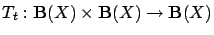 be a sequence of random
operators.
be a sequence of random
operators.
Definition 3.1
A series of value functions
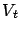
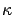
-approximates
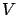
with
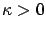
, if
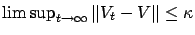
with probability one.
Definition 3.2
We say that
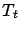
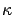
-approximates
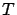
at
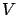
over
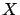
, if
for any
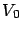
and for
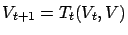
,
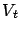
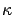
-approximates
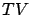
over
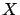
with probability one.
Note that 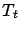 may depend on the approximated value function
may depend on the approximated value function 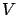 ,
unlike the previous example in Equation 4.
,
unlike the previous example in Equation 4.
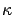 -approximation of value functions is, indeed, weaker (more
general) than probability one uniform convergence: the latter
means that for all
-approximation of value functions is, indeed, weaker (more
general) than probability one uniform convergence: the latter
means that for all
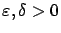 there exists a
there exists a 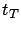 such
that
such
that
whereas an equivalent form of 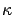 -approximation is that for
all
-approximation is that for
all
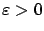 there exists a
there exists a 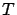 such that
and
such that
and 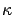 is fixed.
is fixed.
Theorem 3.3
Let
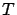
be an arbitrary mapping with fixed point
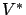
, and let
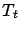
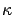
-approximate
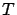
at
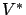
over
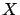
. Let
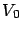
be an
arbitrary value function, and define
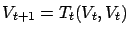
. If
there exist functions
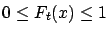
and
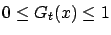
satisfying the conditions below with probability one
- for all
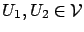 and all
and all 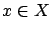 ,
,
- for all
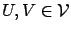 and all
and all 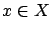 ,
,
- for all
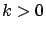 ,
,
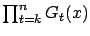 converges to zero uniformly in
converges to zero uniformly in 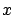 as
as 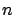 increases;2 and,
increases;2 and,
- there exists
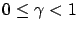 such that for all
such that for all 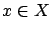 and sufficiently large
and sufficiently large 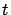 ,
,
then
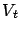
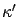
-approximates
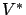
over
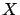
, where
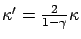
.
Proof.
The proof is similar to that of the original theorem. First we
define the sequence of auxiliary functions
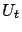
by the recursion
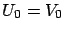
,
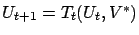
. Since
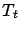
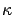
-approximates
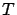
at
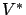
,
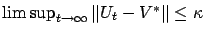
, i.e., for sufficiently large
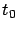
and
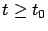
,
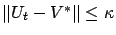
. Let
For
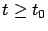
we have
Then, by Lemma
C.1 (found in the appendix), we get
that
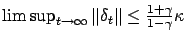
. From this,
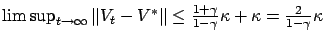
.



Next: Q-learning in Generalized -MDPs
Up: MDPs in Varying Environments
Previous: Generalized -MDPs
![]() -MDPs.
Our definition of closeness both for value functions and
dynamic-programming operators is given below.
-MDPs.
Our definition of closeness both for value functions and
dynamic-programming operators is given below.
![]() be an arbitrary state space and denote by
be an arbitrary state space and denote by
![]() the set of value functions. Let
the set of value functions. Let
![]() be an arbitrary contraction mapping with unique
fixed point
be an arbitrary contraction mapping with unique
fixed point ![]() , and let
, and let
![]() be a sequence of random
operators.
be a sequence of random
operators.
![]() may depend on the approximated value function
may depend on the approximated value function ![]() ,
unlike the previous example in Equation 4.
,
unlike the previous example in Equation 4.
![]() -approximation of value functions is, indeed, weaker (more
general) than probability one uniform convergence: the latter
means that for all
-approximation of value functions is, indeed, weaker (more
general) than probability one uniform convergence: the latter
means that for all
![]() there exists a
there exists a ![]() such
that
such
that