


Next: The AUSTRALIAN data set
Up: Classification with mixtures of
Previous: Classification with mixtures of
A density estimator can be turned into a classifier in two ways, both
of them being essentially likelihood ratio methods. Denote the
class variable by 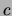 and the set of input variables by
and the set of input variables by 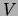 . In the
first method, adopted in our classification experiments under the name
of MT classifier, an MT model
. In the
first method, adopted in our classification experiments under the name
of MT classifier, an MT model 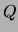 is trained on the domain
is trained on the domain
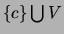 , treating the class variable like any other variable
and pooling all the training data together. In the testing phase, a
new instance
, treating the class variable like any other variable
and pooling all the training data together. In the testing phase, a
new instance
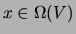 is classified by picking the most
likely value of the class variable given the settings of the other
variables:
is classified by picking the most
likely value of the class variable given the settings of the other
variables:
Similarly, for the MF classifier (termed ``D-SIDE'' by [Kontkanen, Myllymaki, Tirri
1996]), 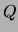 above is an MF trained on
above is an MF trained on
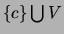 .
The second method calls for partitioning the training set according to
the values of the class variable and for training a tree density estimator
on each partition. This is equivalent to training a mixture of trees
with observed choice variable, the choice variable being the class
.
The second method calls for partitioning the training set according to
the values of the class variable and for training a tree density estimator
on each partition. This is equivalent to training a mixture of trees
with observed choice variable, the choice variable being the class 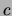 [Chow, Liu 1968,Friedman, Geiger, Goldszmidt
1997]. In particular,
if the trees are forced to have the same structure we obtain the
Tree Augmented Naive Bayes (TANB) classifier of [Friedman, Geiger, Goldszmidt
1997].
In either case one turns to Bayes formula:
[Chow, Liu 1968,Friedman, Geiger, Goldszmidt
1997]. In particular,
if the trees are forced to have the same structure we obtain the
Tree Augmented Naive Bayes (TANB) classifier of [Friedman, Geiger, Goldszmidt
1997].
In either case one turns to Bayes formula:
to classify a new instance 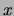 . The analog of the MF classifier in
this setting is the naive Bayes classifier.
. The analog of the MF classifier in
this setting is the naive Bayes classifier.



Next: The AUSTRALIAN data set
Up: Classification with mixtures of
Previous: Classification with mixtures of
Journal of Machine Learning Research
2000-10-19