


Next: The FACES dataset
Up: Density estimation experiments
Previous: Digits and digit pairs
Our second set of density estimation experiments features the ALARM
network as the data generating mechanism [Heckerman, Geiger, Chickering
1995,Cheng, Bell, Liu
1997].
This Bayesian network was constructed from expert knowledge as a medical
diagnostic alarm message system for patient monitoring. The domain
has  discrete variables taking between 2 and 4 values, connected
by 46 directed arcs. Note that this network is not a tree or
a mixture of trees, but the topology
of the graph is sparse, suggesting the possibility of approximating
the dependency structure by a mixture of trees with a small number
of components
discrete variables taking between 2 and 4 values, connected
by 46 directed arcs. Note that this network is not a tree or
a mixture of trees, but the topology
of the graph is sparse, suggesting the possibility of approximating
the dependency structure by a mixture of trees with a small number
of components 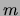 .
We generated a training set having
.
We generated a training set having
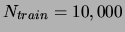 data points and
a separate test set of
data points and
a separate test set of
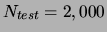 data points. On these sets we
trained and compared the following methods: mixtures of trees (MT),
mixtures of factorial (MF) distributions, the true model, and
``gzip.'' For MT and MF the model order
data points. On these sets we
trained and compared the following methods: mixtures of trees (MT),
mixtures of factorial (MF) distributions, the true model, and
``gzip.'' For MT and MF the model order 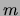 and the degree of
smoothing were selected by cross validation on randomly selected
subsets of the training set.
and the degree of
smoothing were selected by cross validation on randomly selected
subsets of the training set.
Table 3:
Density estimation results for the mixtures of trees and other models
on the ALARM data set. Training set size
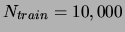 . Average and
standard deviation over 20 trials.
. Average and
standard deviation over 20 trials.
| Model |
Train likelihood |
Test likelihood |
| |
[bits/data point] |
[bits/data point] |
| ALARM net |
13.148 |
13.264 |
Mixture of trees  |
13.51 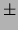 0.04 0.04 |
14.55 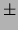 0.06 0.06 |
Mixture of factorials  |
17.11 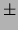 0.12 0.12 |
17.64 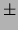 0.09 0.09 |
| Base rate |
30.99 |
31.17 |
| gzip |
40.345 |
41.260 |
The results are presented in Table 3, where
we see that the MT model outperforms the MF model as well as
gzip and the base rate model.
Table 4:
Density estimation results for the mixtures of trees and other models
on a data set of size 1000 generated from the ALARM network.
Average and standard deviation over 20 trials. Recall that
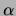 is a smoothing coefficient.
is a smoothing coefficient.
| Model |
Train likelihood |
Test likelihood |
| |
[bits/data point] |
[bits/data point] |
| ALARM net |
13.167 |
13.264 |
Mixture of trees
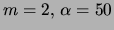 |
14.56 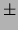 0.16 0.16 |
15.51 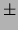 0.11 0.11 |
Mixture of factorials
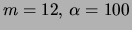 |
18.20 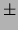 0.37 0.37 |
19.99 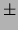 0.49 0.49 |
| Base rate |
31.23 |
31.18 |
| gzip |
45.960 |
46.072 |
To examine the sensitivity of the algorithms to the size of the data
set we ran the same experiment with a training set of size
1,000. The results are presented in Table 4.
Again, the MT model is the closest to the true model.
Notice that the degradation in performance for the
mixture of trees is relatively mild (about 1 bit), whereas the model
complexity is reduced significantly. This indicates the important role
played by the tree structures in fitting the data and motivates the
advantage of the mixture of trees over the mixture of factorials for
this data set.



Next: The FACES dataset
Up: Density estimation experiments
Previous: Digits and digit pairs
Journal of Machine Learning Research
2000-10-19