Consistent Dependency Networks

For several years, we used Bayesian networks to help individuals visualize predictive relationships learned from data. When using this representation in problem domains ranging from web-traffic analysis to collaborative filtering, these individuals expressed a single, common criticism. We developed dependency networks in response to this criticism. In this section, we introduce a special case of the dependency-network representation and show how it addresses this complaint. 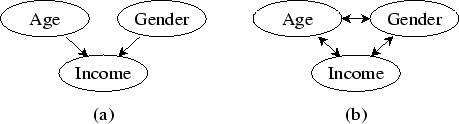Consider Figure 1a, which contains a portion of a Bayesian-network structure describing the demographic characteristics of visitors to a web site. We have found that, when shown graphs like this one and told they represent causal relationships, an untrained person often gains an accurate impression of the relationships. In many situations, however, a causal interpretation of the graph is suspect--for example, when one uses a computationally efficient learning procedure that excludes the possibility of hidden variables. In these situations, the person only can be told that the relationships are ``predictive'' or ``correlational.'' In these cases, we have found that the Bayesian network becomes confusing. For example, untrained individuals who look at Figure 1a will correctly conclude that Age and Gender are predictive of Income, but will wonder why there are no arcs from Income to Age and to Gender--after all, Income is predictive of Age and Gender. Furthermore, these individuals will typically be surprised to learn that Age and Gender are dependent given Income.

Figure 1: (a) A portion of a Bayesian-network structure describing the demographic characteristics of users of a web site. (b) The corresponding consistent dependency-network structure.

Of course, people can be trained to appreciate the (in)dependence semantics of a Bayesian network, but often they lose interest in the problem before gaining an adequate understanding; and, in almost all cases, the mental activity of computing the dependencies interferes with the process of gaining insights from the data. To avoid this difficulty, we can replace the Bayesian-network structure with one where the parents of each variable correspond to its Markov blanket--that is, a structure where the parents of each variable render that variable independent of all other variables. For example, the Bayesian-network structure of Figure 1a becomes that of Figure 1b. Equally important, we do not change the feature of Bayesian networks wherein the conditional probability of a variable given its parents is used to quantify the dependencies. In our experience, individuals are quite comfortable with this feature. Roughly speaking, the resulting model is a dependency network.