Model Averaging for Prediction with Discrete Bayesian Networks

Denver Dash, Gregory F. Cooper; 5(Sep):1177--1203, 2004.

Abstract

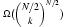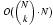In this paper we consider the problem of performing Bayesian model-averaging over a class of discrete Bayesian network structures consistent with a partial ordering and with bounded in-degree k. We show that for N nodes this class contains in the worst-case at least distinct network structures, and yet model averaging over these structures can be performed using operations. Furthermore we show that there exists a single Bayesian network that defines a joint distribution over the variables that is equivalent to model averaging over these structures. Although constructing this network is computationally prohibitive, we show that it can be approximated by a tractable network, allowing approximate model-averaged probability calculations to be performed in O(N) time. Our result also leads to an exact and linear-time solution to the problem of averaging over the 2^N possible feature sets in a naive Bayes model, providing an exact Bayesian solution to the troublesome feature-selection problem for naive Bayes classifiers. We demonstrate the utility of these techniques in the context of supervised classification, showing empirically that model averaging consistently beats other generative Bayesian-network-based models, even when the generating model is not guaranteed to be a member of the class being averaged over. We characterize the performance over several parameters on simulated and real-world data.

[abs][pdf]